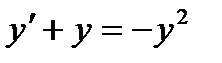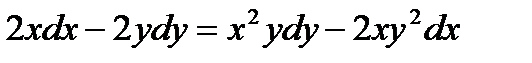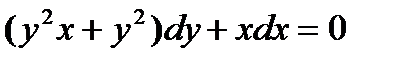Форма обучения: заочная
КОНТРОЛЬНАЯ РАБОТА № 2
Дифференциальное и интегральное исчисление. Дифференциальные уравнения.
Направление подготовки бакалавров 081100.62"Государственное и муниципальное управление";
Профиль "Управление персоналом государственной и муниципальной службы";
Курс, 3 семестр.
Задание № 1. Найти производную функции Для удовлетворительной оценки выполняются задания а)-в), для хорошей и отличной- все пункты а)-д). 1.1 a) б) в) г) 1.2 а) б) в) г) 1.3 а) б) в) г) д) 1.4 а) б) в) г) д) 1.5 а) б) в) г) д) 1.6 а) б) в) г) д) 1.7 а) б) в) г) д) 1.8 а) б) в) г) д) 1.9 а) б) в) г) д) 1.10 а) б) в) г) д) 1.11 а) б) в) г) д) 1.12 а) б) в) г) д) 1.13 а) б) в) г) д) 1.14 а) б) в) г) д) 1.15 а) б) в) г) д) 1.16 а) б) в) г) д) 1.17 а) б) в) г) д) 1.18 а) б) в) г) д) 1.19 а) б) в) г) 1.20 а) б) в) г) д) 1.21 а) б) в) г) д) 1.22 а) б) в) г) д) 1.23 а) б) в) г) д) 1.24 а) б) в) г) д) 1.25 а) б) в) г) д) 1.26 а) б) в) г) д) 1.27 а) б) в) г) д) 1.28 а) б) в) г) д) 1.29 а) б) в) г) д) 1.30 а) б) в) г) д) Задание № 2. Найти производные второго порядка функций заданных: а) явно, б) параметрически, в) неявно. Для удовлетворительной оценки выполняется только задание а), для хорошей и отличной- все пункты а)-в). 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 2.27 2.28 2.29 2.30. Задача № 3. Дана функция z = f(x,y). Найти частные производные первого порядка. 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 3.18 3.19 3.20 3.21 3.22 3.23 3.24 3.25 3.26 3.27 3.28 3.29 3.30 Задание № 4. Найти неопределенные интегралы. Для удовлетворительной и хорошей оценки выполняется только задания а) - с), для отличной- все пункты. 1. а) 2. a) 3. a) 4. a) 5. a) 6. a) 7. a) 8. a) 9. a) 10. a) 11. a) 12. a) 13. a) 14. a) 15. a) 16. a) 17. a) 18. a) 19. a) 20. a) 21. a) 22. a) 23. a) 24. a) 25. a) 26. a) 27. a) 28. a) 29. a) 30. a) 31. a) 32. a)
Задание № 5. Найдите площадь фигуры, ограниченной линиями. Сделать чертеж. 1) y= 2) y= 3) y= 4) y= 5) y= 6) y= 7) y= 8) y= 9) y= 10) y= 11) y= 12) y= 13) y= 14) y= 15) y= 16) y= 17) y=x+5; y= 18) y=x+3; y= 19) y=x+4; y= 20) y= 21) y= 22) 4y= 23) y= 24) y= 25) y= 26) y= 27) y= 28) 29) y= 30) y=
Задание № 6. Решить дифференциальное уравнение с разделяющимися переменными. 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. 6.16. 6.17. 6.18. 6.19. 6.20. 6.21. 6.22. 6.23. 6.24. 6.25. 6.26. 6.27. 6.28. 6.29. 6.30.
|

 .
.


 д)
д) 



 д)
д) 



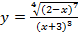




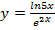
















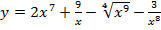



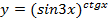






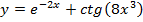






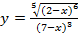








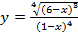








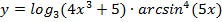





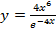

































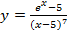















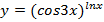
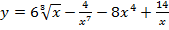


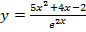










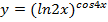

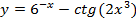





























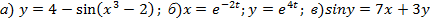

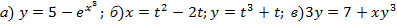

















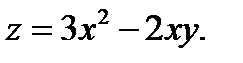



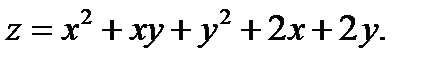







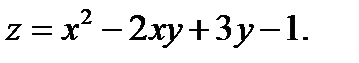
 b)
b)  с)
с)  d)
d) 

 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b) 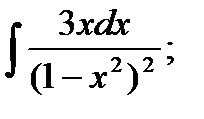 c)
c)  d)
d) 
 b)
b) 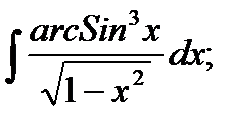 c)
c)  d)
d) 
 b)
b)  c)
c) 

 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
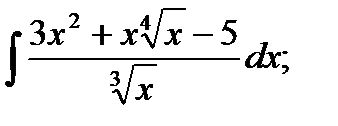 b)
b)  c)
c)  d)
d) 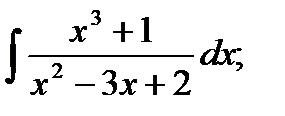
 b)
b)  c)
c)  d)
d) 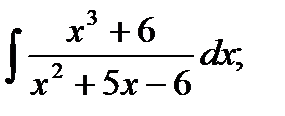
 b)
b) 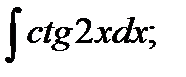 c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
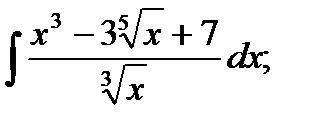 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 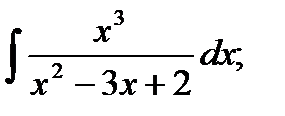
 b)
b) 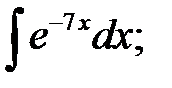 c)
c)  d)
d) 
 b)
b)  c)
c) 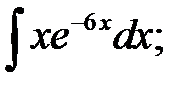 d)
d) 

 y=
y= 
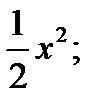 x+2y-6=0;
x+2y-6=0; y=
y= 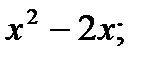
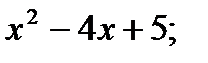 y=2;
y=2; y=2x;
y=2x; y=x+10;
y=x+10; y=
y= 
 y= 2x+2;
y= 2x+2; y=
y= 
 y= -2x+8;
y= -2x+8; y= x-1;
y= x-1; 3y-5x-25=0;
3y-5x-25=0; y=2x-10;
y=2x-10; 2x-y-8=0;
2x-y-8=0; y=2x-6;
y=2x-6; 2x-y-4=0;
2x-y-4=0;


 3y-3x-16=0;
3y-3x-16=0; y=
y= 
 4y=x+6;
4y=x+6; y+3x-4=0;
y+3x-4=0; y=0;
y=0; y=0;
y=0; x=0, y=0;
x=0, y=0; y=0;
y=0; y=3x;
y=3x; y=-2x+8;
y=-2x+8; y=
y=