Анализ схем для обнаружения ситуаций риска
На рис. 11.12, а изображена схема на элементах ИЛИ/И, которую следует проверять на наличие какого-либо риска. Так как схема состоит из элементов ИЛИ и И одновременно, в ней может возникать ситуация статического риска как в нуле, так и в единице. Функция для этой схемы имеет вид
и она может быть развернута следующим образом:
Для того чтобы обнаружить ситуации риска, необходимо при определенных входных условиях рассмотреть, к какой форме сводится развернутое выражение (к При определении временного уравнения схемы некоторыми теоремами алгебры логики нельзя пользоваться. Для преобразования временного уравнения схемы не могут быть применены те правила, в которых используются тождества Если В = 1, С = 0 и D = 1, выражение преобразуется к виду Если В = 1, С = 0 и D = 0, равенство преобразуется к виду Другим способом статический 1-риск может быть обнаружен определением на картах Карно тех комбинаций переменных, при которых значение функции f = 1, как показано на рис. 11.12, б. Анализируя эту карту, можно заметить, что две смежные ячейки 1101 и 0101, отмеченные «1», не покрыты одной и той же первичной импликантой. Включение дополнительной первичной импликанты Для обнаружения статического 0-риска функция должна быть сначала инвертирована и изображена на карте Карно. Рассматриваемая здесь функция имеет вид
Определим двойственную к ней функцию
затем функцию, инверсную к ней:
и, наконец, используя теорему поглощения, приведем ее к следующему виду:
Первые три терма инверсной функции изображены на карте Карно, показанной на рис. 11.12, в. Четвертый (временной) терм не может быть представлен на этой же карте. На карте Карно для инверсной функции можно видеть, что нули в ячейках 1001 и 1011 являются смежными для нулей в ячейках 0001 и 0011, соответственно, и не покрываются одной и той же первичной импликантой. Статический 0-риск устраняется включением дополнительной первичной импликанты для покрытия этих четырех ячеек. Этот терм следует добавить к инверсной функции, которая затем повторно инвертируется для получения функции в гарантированном от риска виде. Анализ схемы, приведенной на рис. 11.12, а, показывает, что в ней могут возникать ситуации риска обоих видов. На практике целесообразнее было бы провести преобразование схемы при помощи карты Карно, показанной на рис. 11.12, б, которая для удобства повторена на рис. 11.12, г. На этой карте функция упрощена таким способом, что в результате получилась гарантированная от статического 1-риска функция. Она имеет следующий вид:
Теперь осталось только проверить изображение на карте Карно инверсной функции для выявления 0-риска. Инверсная функция имеет вид
Она изображена на рис. 11.12, д. Поскольку на этой карте Карно нет смежных нулей, не покрытых одной и той же первичной импликантой, то нет и статического 0-риска, и функция является гарантированной также и от этого типа риска.
|

 ,
, .
.
 , который при обычных обстоятельствах был бы устранен, так как по законам алгебры логики он равен логическому 0. Однако, поскольку А и
, который при обычных обстоятельствах был бы устранен, так как по законам алгебры логики он равен логическому 0. Однако, поскольку А и 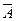 в комбинационных схемах могут быть одновременно равны логической «1», они считаются независимыми переменными в приведенном выражении, полная форма которого необходима для демонстрации переходных процессов.
в комбинационных схемах могут быть одновременно равны логической «1», они считаются независимыми переменными в приведенном выражении, полная форма которого необходима для демонстрации переходных процессов.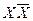 или
или 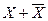 ). Например, если B =0, C = 0 u D = 1,то выражение приводится к
). Например, если B =0, C = 0 u D = 1,то выражение приводится к  . Следовательно, для этих входных условий при изменении А из 0 в 1 появляется статический 0-риск.
. Следовательно, для этих входных условий при изменении А из 0 в 1 появляется статический 0-риск. и
и  . Например, нельзя пользоваться теоремой алгебры логики, согласно которой
. Например, нельзя пользоваться теоремой алгебры логики, согласно которой  , поскольку в ней с помощью тождества
, поскольку в ней с помощью тождества  приводится к форме
приводится к форме  . Выше в этой главе было показано, что А и
. Выше в этой главе было показано, что А и  . Тогда приведенная выше теорема не является справедливой для всех моментов времени.
. Тогда приведенная выше теорема не является справедливой для всех моментов времени. .В этом случае при изменении А от 1 до 0 появляется ситуация статического 1-риска. Следует отметить, что при изменении А от 1 до 0 значение терма
.В этом случае при изменении А от 1 до 0 появляется ситуация статического 1-риска. Следует отметить, что при изменении А от 1 до 0 значение терма  . В этом случае f = 1 независимо от значений А и
. В этом случае f = 1 независимо от значений А и  обеспечит покрытие этих двух ячеек одной и той же первичной импликантой и устранит статический 1-риск.
обеспечит покрытие этих двух ячеек одной и той же первичной импликантой и устранит статический 1-риск. ,
,
 .
. .
. .
.


