Построение гарантированных от риска комбинационных схем

В этом разделе, рассматривается реализация функции

в двух вариантах: а) при помощи элементов И-НЕ и б) при помощи элементов ИЛИ-НЕ. Предположим, что схемы строятся из элементов с максимальным числом входов, равным 3.

Поскольку в первом варианте реализации схемы используются элементы И-НЕ, необходимо получить функцию, гарантированную от статического 1-риска. Сначала следует отразить на карте Карно все те комбинации переменных, при которых функция равна логической «1», как показано на рис. 11.10, а, и упростить их обычным способом. Далее необходимо проверить, нет ли единиц в смежных ячейках, не покрытых одной и той же первичной импликантой. В рассматриваемом случае такими ячейками являются 0111 и 0110 и для устранения непокрытых смежных ячеек добавлена дополнительная первичная импликанта. Единицы, соответствующие дополнительной первичной импликанте, обведены на карте Карно штриховой линией.

Полученная на карте гарантированная от риска функция может быть записана в виде

.

Чтобы удовлетворить условию ограниченности числа входов, это выражение может быть факторизовано, после чего оно примет следующий вид:

.

В результате такой факторизации ситуации риска повторно не возникают. В рассматриваемой задаче риск должен был бы появляться при А = 0, В = 1 и С = 1, а также при изменении D от 1 до 0. При этих условиях факторизованное выражение примет вид

,

т. е. функция удовлетворяет условию устранения риска.

Реализация гарантированной от риска функции с помощью элементов И-НЕ показана на рис. 11.10, б.

Для того чтобы получить гарантированную от риска реализацию данной функции на элементах ИЛИ-НЕ, сначала необходимо изобразить на карте Карно все те комбинации переменных, при которых значение функции равно логическому «0», а затем упростить ее обычным способом. Определенная на нулевых

значениях функция представляет собой инверсию рассматриваемой функции, и карта Карно с ее изображением получается из карты на рис. 11.10, а при помощи заполнения ее свободных ячеек нулями, как показано на рис. 11.11, а.

Наличие, нулей в смежных ячейках, не покрытых одной и той же первичной импликантой, показывает, что упрощенная функция имеет статический 0-риск, обусловливаемый некоторыми определенными ранее условиями. В этом примере такими смежными ячейками являются: а) 0000 и 0001; б) 1000 и 1001. Присоединение дополнительной первичной импликанты ВС позволяет покрыть эти смежные ячейки и удалить 0-риск. Нули, соответствующие дополнительной первичной импликанты, обведены штриховыми линиями на рис. 11.11, а. Полученная на карте инверсная функция имеет вид

.

В результате факторизации, выполняемой для удовлетворения ограничения на число входов у одного элемента, получаем следующую функцию:

.

Найдем двойственную к ней функцию

и затем ее инверсию

.

Реализация этой гарантированной от риска функции с помощью элементов ИЛИ-НЕ показана на рис. 11.11, б.
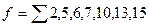
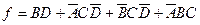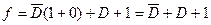
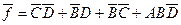
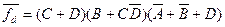