Устранение статического риска
На рис. 11.5 показана схема на элементах И-НЕ, реализующая функцию
Термом согласования для этого уравнения является ВС, который может быть прибавлен к исходному уравнению без изменения его значения. Такое преобразование приведет к следующему выражению:
При условии, что В = С = 1, уравнение упрощается до вида
и даже, если сигналы А и
Таким образом, путем выявления единиц в смежных ячейках карты Карно с изображением функции, не покрытых одной и той же первичной импликантой, можно обнаружить ситуации статического 1-риска. Они могут быть устранены на стадии проектирования схемы включением дополнительных первичных импликант, покрывающих смежные пары ячеек с единицей, не покрытых одной и той же первичной импликантой. Гарантированная от риска схема, реализующая булеву функцию Функция, реализуемая схемой на элементах ИЛИ-НЕ, которая изображена на рис. 11.6, имеет вид
Терм согласования для дополнения этого уравнения имеет вид
Если В = С = 0, то
При включении терма согласования значение функции всегда равно 0 независимо от того, что А и Статический 0-риск устраняется из схемы включением терма согласования
При поиске статического 0-риска на карте Карно необходимо отметить нулевые значения функции. Для получения изображения 0-термов должна быть определена инверсия функции f d. Функция, соответствующая рассматриваемой схеме, имеет вид
Найдем двойственную к f d функцию
и ее инверсию
На рис. 11.9, а показана инверсия функции f d. Можно заметить, что два нуля в смежных ячейках 000 и 100 не покрыты одной и той же первичной импликантой. Включение дополнительной первичной импликанты
Получим двойственную к ней функцию
и ее инверсию
которая представляет собой гарантированную от риска функцию, полученную введением терма согласования, как это было показано ранее. Итак, статический 0-риск может быть выявлен при помощи следующей процедуры: 1) изобразить на карте Карно инверсную функцию; 2) найти смежные ячейки с нулевыми значениями функции, не покрытые одной и той же первичной импликантой; 3) включить дополнительные первичные импликанты для покрытия всех смежных нулевых ячеек, не покрытых одной и той же первичной импликантой; 4) преобразовать функцию путем повторного ее инвертирования в гарантируемую от риска форму.
|

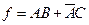 .
.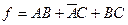 .
.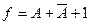
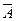 на короткое время становятся равны 0, значение f остается равным 1.
на короткое время становятся равны 0, значение f остается равным 1.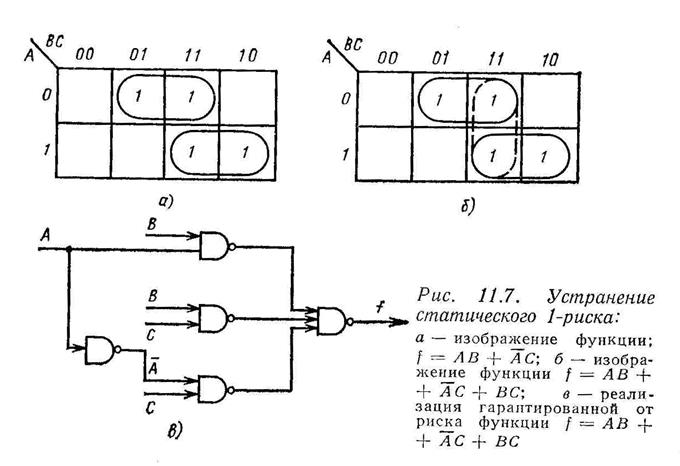
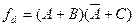 .
. и может быть добавлен к нему без изменения его значения. Таким образом, эта функция принимает вид
и может быть добавлен к нему без изменения его значения. Таким образом, эта функция принимает вид .
.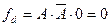 .
.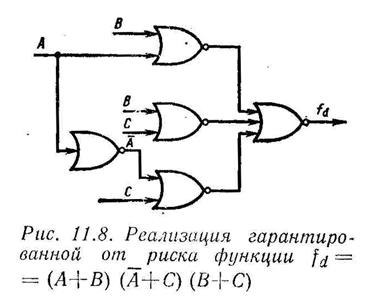 Карта Карно обычно изображается так, что ячейки с единицами соответствуют тем комбинациям переменных, где значение определяемой функции равно 1. Статический 1-риск возникает в схеме, построенной на элементах И-НЕ и изображенной на рис. 11.8, при условии, что А = 1, В = 1, С = 1 и А изменяется до 0. На карте Карно, показанной на рис. 11.7, а, появление риска обусловливается переходом от клетки 111 к клетке 011, что можно установить по наличию единиц в смежных ячейках, не покрытых одной и той же первичной импликантой.
Карта Карно обычно изображается так, что ячейки с единицами соответствуют тем комбинациям переменных, где значение определяемой функции равно 1. Статический 1-риск возникает в схеме, построенной на элементах И-НЕ и изображенной на рис. 11.8, при условии, что А = 1, В = 1, С = 1 и А изменяется до 0. На карте Карно, показанной на рис. 11.7, а, появление риска обусловливается переходом от клетки 111 к клетке 011, что можно установить по наличию единиц в смежных ячейках, не покрытых одной и той же первичной импликантой.
 .
.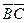 на рис. 11.9, б обеспечивает теперь покрытие смежных нулей одной и той же импликантой.
на рис. 11.9, б обеспечивает теперь покрытие смежных нулей одной и той же импликантой.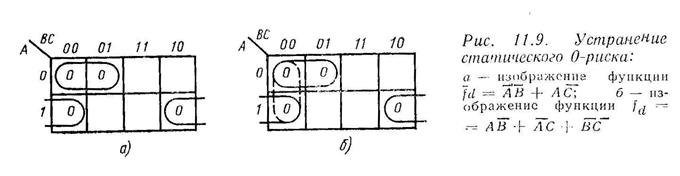
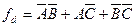 .
.



