Ситуации динамического риска
Второй тип ситуаций риска, появляющихся в комбинационных схемах, называется динамическим риском. Он возникает при изменении выходного сигнала схемы от 0 до 1 или, наоборот, от 1 до 0.
Ситуации динамического риска могут появиться в тех схемах, где сигнал от одной переменной проходит по трем или более путям и каждый из них имеет свое время задержки. Например, функция
может быть реализована с помощью схемы на элементах И и ИЛИ, как показано на рис. 11.14, а. Проверка этой схемы показывает, что сигнал от переменной С может проходить по трем различным путям, и, следовательно, в этой схеме есть вероятность существования динамического риска. Перечислим эти пути: а) через элементы g 1 и g 2; б) через элементы g 3, g 5 и g 2, в) через элементы g 4, g 5 и g 2. Восемь возможных комбинаций переменных А, В и C сведены в таблицу (рис. 11.14, б). Для каждой из этих комбинаций считается, что следующее изменение в ней произойдет с переменной С, как показано в четвертом столбце таблицы. Наличие динамического риска отмечается в последнем столбце.
Однако в том случае, если А = 1, В = 1 и С = 0 и при этом С изменяется от 0 в 1, верхний вход элемента g изменяется от 0 до 1. Другой вход g 2 описывается выражением Проанализировав аналогичным образом все остальные комбинации таблицы, изображенной на рис. 11.14, б, можно установить, что для них ситуация динамического риска не возникает. Если изобразить функцию, реализуемую этой схемой на карте Карно, как показано на рис. 11.14, в, то можно отметить, что в ней отсутствует статический 1-риск. Изображение инверсной функции на карте Карно (рис. 11.14, г) показывает, что в ней также нет и статического 0-риска.
|

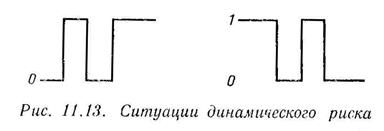 Если при разработке схемы предусмотрено изменение выходного сигнала от 1 до 0, а в действительности его изменение имеет вид 1 ® 0 ® 1 ® 0. то это свидетельствует о наличии в схеме динамического риска. Аналогично этому вместо требуемого изменения выходного сигнала от 0 в 1 при условии динамического риска будет иметь место изменение 0 ® 1 ®0 ® 1. В каждом из этих случаев выходной сигнал изменяется минимум 3 раза, как показано на рис. 11.13.
Если при разработке схемы предусмотрено изменение выходного сигнала от 1 до 0, а в действительности его изменение имеет вид 1 ® 0 ® 1 ® 0. то это свидетельствует о наличии в схеме динамического риска. Аналогично этому вместо требуемого изменения выходного сигнала от 0 в 1 при условии динамического риска будет иметь место изменение 0 ® 1 ®0 ® 1. В каждом из этих случаев выходной сигнал изменяется минимум 3 раза, как показано на рис. 11.13.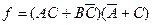

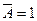 , и этот сигнал является одним из входных для элемента g 1, реализующего функцию ИЛИ. Тем не менее, на выходе этого элемента будет оставаться единичный сигнал независимо от любых изменений, происходящих с С, и, следовательно, выходной сигнал элемента g 2 будет также оставаться неизменным. Поскольку для всех четырех комбинаций изменение сигнала С на входе элемента g 1 не вызывает изменения выходного сигнала для элемента g 2, динамический риск не возникает.
, и этот сигнал является одним из входных для элемента g 1, реализующего функцию ИЛИ. Тем не менее, на выходе этого элемента будет оставаться единичный сигнал независимо от любых изменений, происходящих с С, и, следовательно, выходной сигнал элемента g 2 будет также оставаться неизменным. Поскольку для всех четырех комбинаций изменение сигнала С на входе элемента g 1 не вызывает изменения выходного сигнала для элемента g 2, динамический риск не возникает.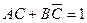 , и, следовательно, выход элемента также изменяется из 0 в 1. При условии t g4 < t g3 следует обратить внимание на результат изменения входного для g 4 сигнала С от 1 до 0. Это изменение вызовет изменение на выходе элемента от 1 до 0, вследствие чего выход элемента g 5 изменится из 1 в 0, а на выходе элемента g 2 произойдет второе изменение сигнала от 1 до 0. Теперь, рассматривая изменение сигнала С от 0 до 8 на входе g 3, можно видеть, что оно приводит к третьему изменению на выходе g 2 от 0 до 1. Эти изменения показаны на функциональной схеме, изображенной на рис. 11.14, а. Очевидно, что при указанных входных условиях, когда С изменяется от 0 до 1, на выходе схемы возникает ситуация динамического риска.
, и, следовательно, выход элемента также изменяется из 0 в 1. При условии t g4 < t g3 следует обратить внимание на результат изменения входного для g 4 сигнала С от 1 до 0. Это изменение вызовет изменение на выходе элемента от 1 до 0, вследствие чего выход элемента g 5 изменится из 1 в 0, а на выходе элемента g 2 произойдет второе изменение сигнала от 1 до 0. Теперь, рассматривая изменение сигнала С от 0 до 8 на входе g 3, можно видеть, что оно приводит к третьему изменению на выходе g 2 от 0 до 1. Эти изменения показаны на функциональной схеме, изображенной на рис. 11.14, а. Очевидно, что при указанных входных условиях, когда С изменяется от 0 до 1, на выходе схемы возникает ситуация динамического риска.


