Пусть функция  определена на отрезке
определена на отрезке 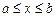 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками  , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке  произвольную точку
произвольную точку  и обозначим через
и обозначим через  длину каждого такого отрезка.
длину каждого такого отрезка.
Определение. Интегральной суммой для функции  на отрезке
на отрезке 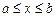 называется сумма вида
называется сумма вида  .
.
Определение. Определенным интегралом от функции  на отрезке
на отрезке 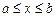 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:  .
.
Для любой функции  , непрерывной на отрезке
, непрерывной на отрезке 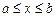 , всегда существует определенный интеграл
, всегда существует определенный интеграл  .
.
Для вычисления определенного интеграла от функции  в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл  , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница:  , то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл  преобразуется с помощью подстановки
преобразуется с помощью подстановки  в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной  . При этом старые пределы интегрирования
. При этом старые пределы интегрирования  и
и  , которые находятся из исходной подстановки:
, которые находятся из исходной подстановки:  ,
,  . Таким образом, имеем
. Таким образом, имеем  .
.
Пример 23. Вычислить определенный интеграл: 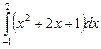 .
.
Решение:
 .
.
Пример 24. Вычислить определенный интеграл:  .
.
Решение:  .
.
Пример 25. Вычислить определенный интеграл: 
 .
.
 .
.
Пример 26. Вычислить определенный интеграл:  .
.
Решение: 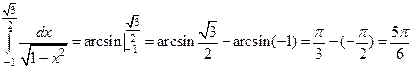 .
.
Пример 27. Вычислить определенный интеграл:  .
.
Решение: положим 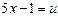 , тогда
, тогда  ,
,  . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования:  ,
,  . Поэтому
. Поэтому
 .
.
Пример 28. Вычислить определенный интеграл:  .
.
Решение: преобразуем подкоренное выражение:  . Положим
. Положим  , откуда
, откуда  . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования:  ,
,  . Следовательно,
. Следовательно,
 .
.

 определена на отрезке
определена на отрезке 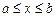 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками  , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке  произвольную точку
произвольную точку  и обозначим через
и обозначим через  длину каждого такого отрезка.
длину каждого такого отрезка. .
. .
. .
. , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница:  , то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования. в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной  . При этом старые пределы интегрирования
. При этом старые пределы интегрирования  и
и  , которые находятся из исходной подстановки:
, которые находятся из исходной подстановки:  ,
,  . Таким образом, имеем
. Таким образом, имеем  .
.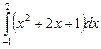 .
. .
. .
. .
.
 .
. .
. .
.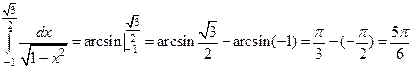 .
. .
.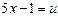 , тогда
, тогда  ,
,  . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования:  ,
,  . Поэтому
. Поэтому .
. .
. . Положим
. Положим  , откуда
, откуда  . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования:  ,
,  . Следовательно,
. Следовательно, .
.


