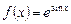Производная сложной функции
Пусть Производная сложной функции находится на основании следующей теоремы: если Эта теорема распространяется и несложные функции, которые задаются с помощью цепочки, содержащей три звена и более. Формулы дифференцирования С – постоянная,
Пример 6. Найти производную функции Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5 и 8: Пример 7. Найти производную функции Решение: применив последовательно формулы 4, 3, 5 и 8, имеем
Пример 8. Найти производную функции Решение. Применяя формулы 6, 3, 7 и 1, получим:
Пример 9. Найти производную функции Решение. Это сложная функция с промежуточным аргументом Вычислим значение производной при
Пример 10. Найти производную функции Решение. Используя правило дифференцирования произведения и соответствующие формулы нахождения производных, получим
Пример 11. Найти производную функции Решение: используя правило дифференцирования частного и соответствующие формулы нахождения производных, получим
Пример 12. Найти производную функции Решение: полагая
Пример 13. Найти производную функции Решение.
Производные высших порядков Производная функции Второй производной функции Вторая производная функции обозначается одним из символов: Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка: Пример 14. Найти вторую производную функции Решение. Сначала найдем первую Дифференцируя еще раз, найдем вторую производную: Пример 15. Найти вторую производную функции Решение. Сначала найдем первую производную этой сложной функции: Дифференцируя еще раз, найдем вторую производную:
|

 , где
, где  является не независимой переменной, а функцией независимой переменной
является не независимой переменной, а функцией независимой переменной  , т.е.
, т.е.  . Таким образом,
. Таким образом, 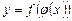 .В этом случае функция
.В этом случае функция  называется сложной функцией
называется сложной функцией 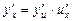
 и
и  функции аргумента
функции аргумента 
















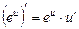




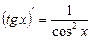





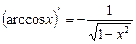





 .
.
 .
.
 .
. .
.
 и вычислить ее значение при
и вычислить ее значение при 
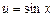 . Используя формулы 8а и
. Используя формулы 8а и  13, имеем:
13, имеем:  .
. .
. .
. .
.
 .
. , получим
, получим  .
.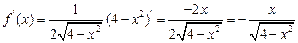
 .
.
 в общем случае является функцией от
в общем случае является функцией от  .
.  ,
,  ,
,  .
. ,
,  ,
,  .
. .
. производную:
производную: .
.