Общие теоретические сведения. № Название команд КС Момент
ОТ 20 июля 2015 года
КС – сокращенное название команды; КПО – количество правильных ответов; М – место, занятое в игре; О – очки за игру. ПРОТОКОЛ I Парковая игра по КЧГК «КЛУБА ИНТЕЛЕКТУАЛЬНЫХ ИГР» РГРТУ ОТ 6 июля 2015 года
КС – сокращенное название команды; КПО – количество правильных ответов; М – место, занятое в игре; О – очки за игру. ПРОТОКОЛ V Парковая игра по КЧГК «КЛУБА ИНТЕЛЕКТУАЛЬНЫХ ИГР» РГРТУ ОТ 17 августа 2015 года
КС – сокращенное название команды; КПО – количество правильных ответов; М – место, занятое в игре; О – очки за игру.
ЛАБОРАТОРНАЯ РАБОТА № 3. ИССЛЕДОВВАНИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ АКТИВНОГО И ИНДУКТИВНОГО СОПРОТИВЛЕНИЙ Цель работы: Экспериментальное исследование характера изменения тока, мощности и падений напряжений на участках последовательной цепи, состоящей из активного и индуктивного сопротивлений, а также построение круговой диаграммы. Общие теоретические сведения Ток в катушке индуктивности отстает от напряжения на ней на угол 900. Действующее значение тока, протекающего через катушку индуктивности связано с действующим значением напряжения на ней формулой, выражающей закон Ома для катушки индуктивности на переменном токе:
Величина
Действующее значение напряжения определяется:
Отсюда можно определить ток в цепи:
Выражение
Активная мощность в цепи рис. 3.1,а и 3.1,б определяется:
Рис.3.1. Принципиальные схемы (а, б) и векторные диаграммы (в, г) цепи RL. Изменение активного и индуктивного сопротивлений по разному влияет на изменение активной мощности цепи. При постоянном значении индуктивности и увеличении R от нуля до бесконечности, активная мощность растет, достигает максимума и далее уменьшается. Чтобы найти значение R, при котором активная мощность максимальная, надо приравнять к нулю первую производную активной мощности по активному сопротивлению, т. е. положить
Из этого условия получим R = XL. При этом соотношении мощность в цепи максимальная. При постоянном значении сопротивления R c увеличением XL от нуля до бесконечности активная мощность цепи монотонно уменьшается, стремясь к нулю. При изменении R и неизменном L (или при изменении L и неизменном R) геометрическим местом концов вектора тока является полуокружность. Геометрическим местом концов векторов UR и UL также является полуокружность (рис.3.1,в и 3.1,г). Рассмотрим подробнее построение круговой диаграммы для цепи RL. Учтем, что реальная катушка индуктивности обладает активным сопротивлением r и будем считать, что индуктивность катушки L, а, следовательно, и индуктивное сопротивление XL=ωL, также как и внутреннее сопротивление катушки r нам известны. Для построения круговой диаграммы для случая R = const, r=const, L = var (XL=var) (рис. 3.2) задаемся масштабами по напряжению, току и сопротивлению: m U; m l; m Z. От точки 0 по оси ординат откладываем в принятом масштабе вектор напряжения
Ток
Рис.3.2. Электрическая цепь с последовательным включением элементов RL (а) и ее круговая диаграмма при R =const, r=const и XL=var (б). В масштабе m Z откладываем по направлению вектора Тогда электрические величины определяются: I = m lOM; P = m рOF; UL = m UOD; Q = m QMF; UR+r = m UDE; S = m SOM;
Отметим одну особенность круговой диаграммы. Напряжения UL (отрезок OD) и UR+r (отрезок DE) реально измерить мы не можем. Вольтметры в схеме на рис.3.4 и 3.5 измеряют напряжение UR на резисторе R и напряжение Uк на катушке индуктивности. Сопротивление r является внутренним сопротивлением катушки индуктивности. Напряжение на нем нельзя замерить. Измеряемое напряжение на катушке Uк (отрезок OB) является геометрической суммой двух напряжений UR=mU·BE, Uк=mU·OB
Рис.3.3. Электрическая цепь с последовательным включением элементов RL (а) и ее круговая диаграмма при XL =const, r=const и R=var (б). На рис.3.3 приведена круговая диаграмма для случая, когда XL=const, r=const и R=var. Для построения круговой диаграммы в этом случае также задаемся масштабами по напряжению, току и сопротивлению: m U; m l; m Z. От точки 0 по оси абсцисс откладываем в принятом масштабе вектор напряжения
Ток В масштабе m Z откладываем по направлению вектора Тогда электрические величины определяются: I = m lOM; P = m рOF; UL = m UOD; Q = m QMF; S = m SOM; Ur = m UDB; UR = m UBE; Uк = m UOB;
Измеряемое напряжение на катушке Uк (отрезок OB) является геометрической суммой двух напряжений UR=mU·BE, Uк=mU·OB.
Рис.3.4. Вид активного окна лабораторной работы №3.1. Принципиальная схема, волновые и векторные диаграммы цепи RL при R =const, r=const и L=var (б). Порядок выполнения работы 1. Исследовать схему, содержащую последовательно включенные элементы R и L. Параметры схемы устанавливает компьютер по шифру студента (по двум последним цифрам). Напряжение на входе схемы автоматически поддерживается во время опыта постоянным. 2. Исследовать работу схемы (рис.3.4) при постоянном значении активного сопротивления R, изменяя величину индуктивности катушки от максимального значения до нуля. Для этих измерений следует выбрать лабораторную работу ”3.1. Последовательное соединение RL (R=const, r=const, L=var)” (рис.3.4) Данные записать в таблицу 3.1. Наблюдать по осциллограмме как изменяются мгновенные значения тока в цепи и мощности. Формулы для расчетов:
r=R+r –R;
Рис.3.5. Вид активного окна лабораторной работы №3.2. Принципиальная схема, волновые и векторные диаграммы цепи RL при L =const, r=const и R=var (б).
Таблица 3.1
3. Исследовать работу схемы (рис.3.5) при изменении активного сопротивления цепи от R = 0 до R = max; меняя ток через 0,1 А. Для этих измерений следует выбрать лабораторную работу ”3.2. Последовательное соединение RL (L=const, r =const, R=var)” (рис.3.5). Данные свести в таблицу 3.2. Таблица 3.2
4. Для одного из пунктов по указанию преподавателя построить векторные диаграммы напряжений и токов. 5. Результаты расчетов занести сначала для проверки в таблицу 3.3 в компьютере (вызвав ее из меню), а затем в такую же таблицу в отчете; Таблица 3.3
6. Построить в одних осях координат по данным п. 2 (табл.3.1) зависимости: I; UR ; Uк ; P; cos j; Z = f (XL) и в других осях координат по данным п. 3 (табл.3.2) зависимости: I; UR; Uк; P; cos j; Z = f (R). 7. Построить круговую диаграмму токов и напряжений по данным опыта п.2 или п. 3 по указанию преподавателя. Рассчитать по круговой диаграмме UR; Uк; P и сравнить их с величинами, полученными в табл. 3.1 или табл. 3.2, для замера, указанного преподавателем. Контрольные вопросы 1. Написать выражение закона Ома для последовательного соединения элементов R и L. 2. Построить векторную диаграмму для последовательного соединения R и L. Почему U меньше арифметической суммы UR и UL? 3. Записать выражение общего сопротивления для последовательного соединения R и L. Почему уменьшается cos j при увеличении индуктивного сопротивления? 4. Как изменяется ток этой цепи при: а) изменении L от 0 до ¥ и R =const? б) изменении R от 0 до ¥ и С =const? Записать выражение для наибольшего и наименьшего значения тока в случаях “а” и “б”. Почему уменьшается UR при увеличении L?. 5. Сформулировать правила построения круговых диаграмм напряжения и тока. 6. Как по круговой диаграмме определить для данного значения сопротивления R - ток, напряжения UR и Ur, активную, реактивную и полную мощности. 7. Как изменяются активная и реактивная мощности при изменении R от 0 до ¥? 8. Как изменяются: общее сопротивление цепи Z и активная и реактивная составляющие тока при изменении R от 0 до ¥? 9. В цепи, изображенной на рис.3.6. известны: U =50 В, UR =30 В.
|

 (3.1)
(3.1)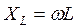 называется индуктивным сопротивлением. При прохождении синусоидального тока по цепи, изображенной на рис. 3.1,а и 3.1,б, ток в любом сечении цепи один и тот же, а общее напряжение, согласно второму закону Кирхгофа, равно геометрической сумме падений напряжений на активном и индуктивном сопротивлениях:
называется индуктивным сопротивлением. При прохождении синусоидального тока по цепи, изображенной на рис. 3.1,а и 3.1,б, ток в любом сечении цепи один и тот же, а общее напряжение, согласно второму закону Кирхгофа, равно геометрической сумме падений напряжений на активном и индуктивном сопротивлениях: (3.2)
(3.2) (3.3)
(3.3) (3.4)
(3.4) называется полным сопротивлением цепи. В такой цепи ток отстает по фазе от напряжения на угол
называется полным сопротивлением цепи. В такой цепи ток отстает по фазе от напряжения на угол (3.5)
(3.5)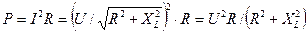 (3.6)
(3.6)
 или
или . (3.7)
. (3.7) (отрезок ОЕ). Находим значение тока
(отрезок ОЕ). Находим значение тока  при коротком замыкании на зажимах изменяющегося индуктивного сопротивления, т.е. при XL = 0
при коротком замыкании на зажимах изменяющегося индуктивного сопротивления, т.е. при XL = 0 (3.8)
(3.8)
 m р = m Q = m S = m lU.
m р = m Q = m S = m lU. и
и  Точка B также перемещается по окружности. Диаметр этой окружности GE находится из соотношения
Точка B также перемещается по окружности. Диаметр этой окружности GE находится из соотношения  . Разделив отрезок GE пополам, найдем центр CU’ этой окружности. Измеряемые напряжения будут равны:
. Разделив отрезок GE пополам, найдем центр CU’ этой окружности. Измеряемые напряжения будут равны: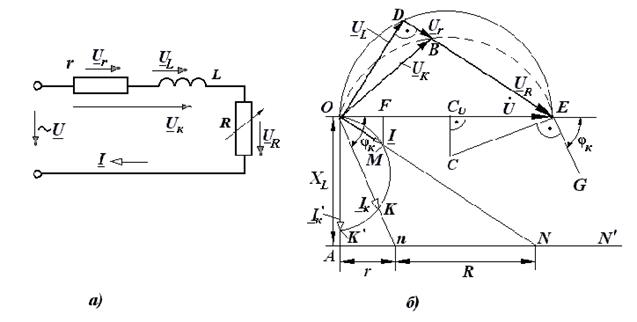
 при R = 0 и r =0.
при R = 0 и r =0. (3.9)
(3.9)
 ;
;  ;
;  ;
;  ;
; ;
; 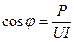 ;
;




