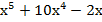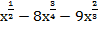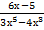ПРОИЗВОДНАЯ ФУНКЦИИ

1. Найдите производную функции у = 4

2. Найдите производную функции у = 7

3. Найдите производную функции у = 8

4. Найдите производную функции у = 12

5. Найдите производную функции у = 4

6. Найдите производную функции у = 14

7. Найдите производную функции у = 4

8. Найдите производную функции у = 10

9. Найдите производную функции у = (2х⁴-3)(6х³+2х)

10. Найдите производную функции у = (3х⁷+5х)(4х³-3х²)

11. Найдите производную функции у = (5х³-4х⁸)(2х⁴-5х)

12. Найдите производную функции у = (7х⁵+8х³)(5х²-х)

13. Найдите производную функции у = (2х⁶-3х+2)(3х³+х)

14. Найдите производную функции у = (5х⁴+3х⁵)(8х³-12х-1)

 

15. Найдите производную функции

 

16. Найдите производную функции

 

17. Найдите производную функции

 

18. Найдите производную функции

19. Напишите уравнение касательной к графику функции f(x) = x⁵+x³+1 в точке с абсциссой х₀ = 1.

20. Напишите уравнение касательной к графику функции f(x) = 4x⁴-16x²+10 в точке с абсциссой х₀ = -1.

21. Напишите уравнение касательной к графику функции f(x) = 3x⁴+24x-11 в точке с абсциссой х₀ = 2.

22. Напишите уравнение касательной к графику функции f(x) = 5x^3_15x-3 в точке с абсциссой х₀ = -2.

23. Напишите уравнение касательной к графику функции f(x) = -6x²+4x+21 в точке с абсциссой х₀ = -3.

24. Напишите уравнение касательной к графику функции f(x) = -7x²-21x+1 в точке с абсциссой х₀ = 4.

25. Найдите интервалы монотонности и экстремумы функции f(x) = х² – 10х + 11

26. Найдите интервалы монотонности и экстремумы функции f(x) = 3х² – 18х + 23

27. Найдите интервалы монотонности и экстремумы функции f(x) = 9х² + 9х - 41

28. Найдите интервалы монотонности и экстремумы функции f(x) = -4х² – 32х + 7

29. Найдите интервалы монотонности и экстремумы функции f(x) = -5х² + 20х - 311

30. Найдите интервалы монотонности и экстремумы функции f(x) = х³ – 3х

31. Найдите интервалы монотонности и экстремумы функции f(x) = х³ + 6х +4

32. Найдите интервалы монотонности и экстремумы функции f(x) = 2х³ – 30х - 44

33. Найдите интервалы монотонности и экстремумы функции f(x) = 10х³ – 6х + 32

34. Найдите интервалы монотонности и экстремумы функции f(x) = х⁴ – 2х²

35. Найдите интервалы монотонности и экстремумы функции f(x) = х⁴ +12х² + 3

36. Найдите интервалы монотонности и экстремумы функции f(x) = 3х⁴ – 10х² -35

37. Вычислите: 5f '(2) – 3f(-1) + 2f(0), если f(x) = 4x³ – 2x² + 4

38. Вычислите: 2f '(-3) + 3f '(2) - 4f(1), если f(x) = 2x³ – 3x² – 5х

39. Вычислите: 7f (0) – 4f (-1) + 5f '(-3), если f(x) = 4x³ + 8x² – 3х

40. Вычислите: f '(5) – 2f(1) - 6f '(-2), если f(x) = 2x⁴ – 5x² + 7

41. Вычислите: 10f '(0) + 4f(-1) - f(2), если f(x) = x⁵ – 3x³ + х

42. Вычислите: 2f '(1) – 5f '(2) + 3f(-1), если f(x) = 6x⁴ + 9x + 11

43. Решите уравнение: f '(х) = 20, если f(х) = 10х² + 60х - 19

44. Решите уравнение: f '(х) = 12, если f(х) = 6х² - 24х + 33

45. Решите уравнение: f '(х) = 8, если f(х) = 5х² - 22х - 56

46. Решите уравнение: f '(х) = - 14, если f(х) = 3х² + 4х - 48

47. Решите уравнение: f '(х) = - 4, если f(х) = 11х² - 48х + 13

48. Вычислите f ΄(-2), f ΄(3), f ΄(1), если f (х) = 4х²-5х+3

49. Вычислите f ΄(4), f΄(-5), f΄(-1), если f(х)=2х³+3х – 10

50. Вычислите f΄(-3), f΄(0), f΄(2), если f(х) = 5х⁴ – 8х³ + х