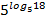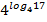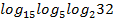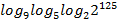ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ.
1. Найдите значение выражения 2. Найдите значение выражения 3. Найдите значение выражения 4. Найдите значение выражения 5. Найдите значение выражения 6. Найдите значение выражения 7. Найдите значение выражения 8. Найдите значение выражения log6198 – log65,5 9. Найдите значение выражения log12108 – log120,75 10. Найдите значение выражения log12216 – log121,5 11. Найдите значение выражения log8112 – log81,75 12. Найдите значение выражения log832 – log8 13. Найдите значение выражения log1112,1 + log1110 14. Найдите значение выражения log56,25 + log54 15. Найдите значение выражения log35,4 + log35 16. Найдите значение выражения 17. Найдите значение выражения 18. Найдите значение выражения 19. Найдите значение выражения 20. Найдите значение выражения 21. Найдите значение выражения 22. Найдите значение выражения 23. Найдите значение выражения 24. Найдите значение выражения 25. Найдите значение выражения 26. Найдите значение выражения 27. Найдите значение выражения 28. Найдите значение выражения 29. Найдите значение выражения 30. Найдите значение выражения lg 0,0001+ 100 31. Найдите значение выражения lg 1000 – 2 32. Найдите значение выражения lg 100 + 4 33. Найдите значение выражения lg 0,00001 – 0,6 34. Найдите значение выражения 35. Найдите значение выражения 36. Вычислите 18∙ 37. Вычислите 4 ∙ 38. Вычислите 20 ∙ 39. Вычислите 4 ∙ 40. Вычислите 11 ∙ 41. Вычислите 15 ∙ 42. Вычислите 10 ∙ 43. Вычислите 44. Вычислите 45. Вычислите 46. Вычислите 47. Вычислите
|


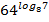


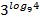
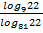




 +
+ 

 27 +
27 + 


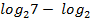 63 +
63 + 
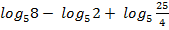
 25 +
25 + 



 - 2
- 2