Коэффициенты y для двутавровых балок с двумя осями симметрии
| Количество закреплений сжатого пояса в пролете
| Вид нагрузки в пролете
| Нагруженный пояс
| Формулы для y при значениях a
| | 0,1 £ a £ 40
| 40 < a £ 400
| | Без закреплений
| Сосредоточенная
| Верхний
Нижний
| y = 1,75 + 0,09 a
y = 5,05 + 0,09 a
| y = 3,3 + 0,053 a - 4,5 × 10-5 a 2
y = 6,6 + 0,053 a - 4,5 × 10-5 a 2
| | Равномерно распределенная
| Верхний
Нижний
| y = 1,6 + 0,08 a
y = 3,8 + 0,08 a
| y = 3,15 + 0,04 a - 2,7 × 10-5 a 2
y = 5,35 + 0,04 a - 2,7 × 10-5 a 2
| | Два и более, делящих пролет на равные части
| Любая
| Любой
| y = 2,25 + 0,07 a
| y = 3,6 + 0,04 a - 3,5 × 10-5 a 2
| | Одно в середине
| Сосредоточенная в середине
| Любой
| y = 1,75 y 1
| y = 1,75 y 1
| | Сосредоточенная в четверти
| Любой
| y = 1,14 y 1
y = 1,6 y 1
| y = 1,14 y 1
y = 1,6 y 1
| | Равномерно распределенная
| Верхний
Нижний
| y = 1,14 y 1
y = 1,6 y 1
| y = 1,14 y 1
y = 1,6 y 1
| Примечание. Значение y 1 следует принимать равным y при двух и более закреплениях сжатого пояса в пролете.
Таблиця 3
| d
| £ 0,8
| 1,0
| 2,0
| 4,0
| 6,0
| 10,0
| ³ 30
| | ccr
| 30,0
| 31,5
| 33,3
| 34,6
| 34,6
| 35,1
| 35,5
|
Таблиця 4
| Балки
| d
| Предельные значения slocs при a / hef, равном
| | 0,8
| 0,9
| 1,0
| 1,2
| 1,4
| 1,6
| 1,8
| ³ 2,0
| | Сварные
| £ 1
|
| 0,146
| 0,183
| 0,267
| 0,359
| 0,445
| 0,540
| 0,618
| |
|
| 0,109
| 0,169
| 0,277
| 0,406
| 0,543
| 0,652
| 0,799
| |
|
| 0,072
| 0,129
| 0,281
| 0,479
| 0,711
| 0,930
| 1,132
| |
|
| 0,066
| 0,127
| 0,288
| 0,536
| 0,874
| 1,192
| 1,468
| |
|
| 0,059
| 0,122
| 0,296
| 0,574
| 1,002
| 1,539
| 2,154
| | ³ 30
|
| 0,047
| 0,112
| 0,300
| 0,633
| 1,283
| 2,249
| 3,939
| | На высокопрочных болтах
| -
|
| 0,121
| 0,184
| 0,378
| 0,643
| 1,131
| 1,614
| 2,347
|
Таблиця 5
| hef
| £ 0,8
| 0,9
| 1,0
| 1,2
| 1,4
| 1,6
| 1,8
| ³ 2,0
| | c 2
| По табл. 21, т. е. c 2 = ccr
| 37,0
| 39,2
| 45,2
| 52,8
| 62,0
| 72,6
| 84,7
|
Таблиця 6
| d
| Значение c 1 для сварных балок при a / hef, равном
| | £ 0,5
| 0,6
| 0,8
| 1,0
| 1,2
| 1,4
| 1,6
| 1,8
| ³ 2,0
| | £ 1
| 11,5
| 12,4
| 14,8
| 18,0
| 22,1
| 27,1
| 32,6
| 38,9
| 45,6
| |
| 12,0
| 13,0
| 16,1
| 20,4
| 25,7
| 32,1
| 39,2
| 46,5
| 55,7
| |
| 12,3
| 13,3
| 16,6
| 21,6
| 28,1
| 36,3
| 45,2
| 54,9
| 65,1
| |
| 12,4
| 13,5
| 16,8
| 22,1
| 29,1
| 38,3
| 48,7
| 59,4
| 70,4
| |
| 12,4
| 13,6
| 16,9
| 22,5
| 30,0
| 39,7
| 51,0
| 63,3
| 76,5
| | ³ 30
| 12,5
| 13,7
| 17,0
| 22,9
| 31,0
| 41,6
| 53,8
| 68,2
| 83,6
|
Додаток 5
Таблиця 1
| Характеристика расстояния
| Расстояния при размещении болтов
| | 1. Расстояния между центрами болтов в любом направлении:
|
| | а) минимальное
| 2,5 d *
| | б) максимальное в крайних рядах при отсутствии окаймляющих уголков при растяжении и сжатии
| 8 d или 12 t
| | в) максимальное в средних рядах, а также в крайних рядах при наличии окаймляющих уголков:
|
| | при растяжении
| 16 d или 24 t
| | при сжатии
| 12 d или 18 t
| | 2. Расстояния от центра болта до края элемента:
|
| | а) минимальное вдоль усилия
| 2 d
| | б) то же, поперек усилия:
|
| | при обрезных кромках
| 1,5 d
| | при прокатных кромках
| 1,2 d
| | в) максимальное
| 4 d или 8 t
| | г) минимальное для высокопрочных болтов при любой кромке и любом направлении усилия
| 1,3 d
|
Додаток 6
Таблиця 1
Коэффициенты j продольного изгиба центрально-сжатых элементов
| Гибкость, l
| Коэффициенты j для элементов из стали с расчетным сопротивлением Ry, МПа (кгс/см2)
| | 200 (2050)
| 240 (2450)
| 280 (2850)
| 320 (3250)
| 360 (3650)
| 400 (4100)
| 440 (4500)
| 480 (4900)
| 520 (5300)
| 560 (5700)
| 600 (6100)
| 640 (6550)
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| Примечание. Значение коэффициентов j в таблице увеличены в 1000 раз.
Таблиця 2
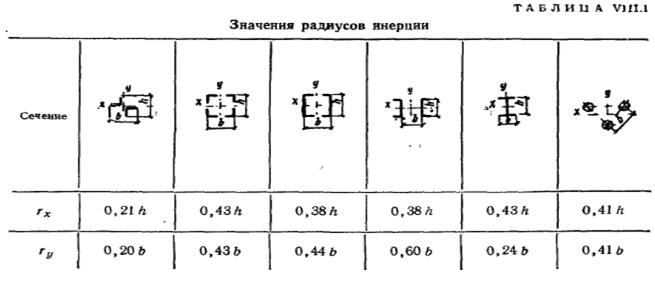
Таблиця 3
|
Клас стали
|
С 38\23
|
С 44\29
|
С 46\33
С 52\40
|
С 60\45
|
С 70\60
|
С85\70
| |
Qум
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
Значення умовної сили Qум, кН
Таблиця 4

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
|
Классификация холодных блюд и закусок. Урок №2 Тема: Холодные блюда и закуски. Значение холодных блюд и закусок. Классификация холодных блюд и закусок. Кулинарная обработка продуктов...
ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики...
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
|
|





