Транспортная задача линейного программирования. Исходные параметры модели транспортной задачи
Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукции однородного груза из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции. Исходные параметры модели транспортной задачи n – количество пунктов отправления; m – количество пунктов назначения; Qi – запас в пункте отправления Ai (i = 1,2…n); bj – спрос на продукцию в пункте назначения Bj (j = 1,2…m); Cij – тариф (стоимость) перевозки единицы продукции из пункта отправления Ai в пункт назначения Bj; Xij – количество продукции, перевозимой из пункта отправления Ai в пункт назначения Bj; F(х) – транспортные расходы на перевозку всей продукции (р.). Транспортная модель
Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа (1) ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа (2) ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворять спрос на продукцию в этом пункте. Наглядной формой транспортной задачи является транспортная матрица.
Общий вид транспортной матрицы
Из модели следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е.
Если это условие выполняется, то транспортная задача называется закрытой, а в противном случае - открытой. Рассмотрим вариант стандартной транспортной задачи Пример. С двух складов нужно перевезти однородный груз в три магазина. На I складе имеется 1800 т груза; На II складе имеется 2600 т груза. В магазин № 1 нужно доставить 1000 т; В магазин № 2 нужно доставить 1200 т; В магазин № 3 нужно доставить 2200 т.
Таблица - Тариф (стоимость) перевозки 1 т груза, тыс. руб.
Требуется определить такой план перевозок, при котором весь груз будет доставлен в указанных количествах в каждый магазин с минимальными затратами на перевозку. Обозначим Xij – количество груза, которое необходимо перевезти от i – го поставщика (склада) к j – му потребителю (магазину) i = 1,2 j = 1,2,3. X11 – объем груза, перевозимого c I склада в магазин № 1, т; Х12 - объем груза, перевозимого cо II склада в магазин № 2, т; Х13 - объем груза, перевозимого c III склада в магазин № 3, т; Х21 - объем груза, перевозимого cо II склада в магазин № 1, т; Х22 - объем груза, перевозимого cо II склада в магазин № 2, т; Х23 - объем груза, перевозимого cо II склада в магазин № 3, т.
Ограничения: 1) по возможности I склада, т х11 + х12 + х13 = 1800 2) по возможности II склада, т х21 + х22 + х23 = 2600 3) по потребности магазина № 1, т х11 + х21 = 1000 4) по потребности магазина № 2, т х12 + х22 = 1200
4400 т = 4400 т Целевая функция F(x) = 2х11 + 2х12 + 3х13 + 3х21 + 4х22 + 2х23 →min
Решение: Вначале принимается исходный вариант перевозок, а затем последовательно производится его улучшение до получения оптимального плана. Для получения первоначального исходного плана перевозок используем правило «северо-западного» угла, т.е. вначале максимально допустимое количество груза помещается в верхнюю левую клетку 91 строка 1 столбец, затем заполняется соседняя клетка и т.д. до распределения всего количества груза. При этом количество занятых клеток составит: m + n – 1 = 2 + 3 – 1 = 4, где m – количество поставщиков: n – количество потребителей. Первоначальный план представлен в следующей таблице:
х11 = 1000 т х22 = 400 т х12 = 800 т х23 = 2200 т
F (x) = 2*1000 + 2*800 + 4*400 + 2*2200 = 9600 т. р
|

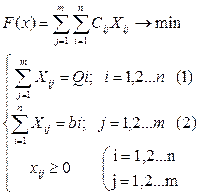
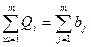
 1000
1000
 800
800



