Симплекс-метод решения задач линейного программирования
Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому, при этом значение целевой функции изменяется. Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота. Коммерческое предприятие реализует “n” товарных групп, располагая “m” ограниченными материально-денежными ресурсами Математическую модель задачи запишем следующим образом. Определить вектор
хj
и обеспечить максимальное значение целевой функции f(х) = Пример:Коммерческое предприятие, располагающее материально-денежными ресурсами, реализует три группы товара А, В и С. Плановые нормативы затрат ресурсов на 1 тыс. руб. товарооборота, доход от продажи товаров на 1 тыс. руб. товарооборота, а также объем ресурсов заданы в следующей таблице:
Определить плановый объем продажи товаров так, чтобы доход торгового предприятия был максимальный. Переменные: х1 – количество товаров группы А, ед. х2 – количество товаров группы В, ед. х3 – количество товаров группы С, ед. Ограничения: 1) По использованию рабочего времени продавцов, чел-ч. 0,1х1+0,2х2+0,4х3 2) По использованию площадей торговых залов, м2 0,05х1+0,02х2+0,02х3 3) По использованию площадей складских помещений, м2 3х1+х2+2х3 4) Условие не отрицательности переменных х1 Целевая функция: Максимальное значение целевой функции, тыс. руб. f(х) = 3х1+5х2+4х3
Алгоритм симплексного метода включает следующие этапы: 1.Составление первого опорного плана
Система ограничений задачи, решаемой симплексным методом задана в виде неравенств смысла “
0,05х1+0,02х2+0,02х3+х5 = 120 3х1+х2+2х3+х6 = 8000
Матрица коэффициентов А=(а ij) этой системы уравнений имеет вид:
Решим систему уравнений относительно базисных переменных:
х5 = 120 – (0,05х1+0,02х2+0,02х3) х6 = 8000 – (3х1+х2+3х3) Функцию цели запишем в виде уравнения f(х) = 0 – (-3х1 – 5х2 – 4х3). Полагая что основные переменные х1=0 х2=0 х3=0, получим первый опорный план, х4= в 1; х5= в 2; х6= в 3 f(x) =0; который заносим в симплексную таблицу № 1. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположным знаком:
2. Проверка плана на оптимальность Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны ( Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план неоптимальный и его можно улучшить. Первый опорный план, представленный в первой симплексной таблице неоптимальный, т.к. в индексной строке находятся отрицательные коэффициенты: -3; -5; -4. Полагая что основные переменные х1=0; х2=0;х3=0, а дополнительные переменные х4=1100; х5=120; х6=800; f(x)=0. Следовательно, товары не продаются, а ресурсы не используются, доход равен нулю. В этом случае переходим к следующему этапу алгоритма. 3. Определение ведущих столбца и строки Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что и определяет ведущий столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные. Затем элементы столбца свободных членов симплексной таблицы делим на положительные элементы ведущего столбца. Результаты заносим в отдельный столбец( Элемент симплексной таблицы, находящийся на пересечении ведущих столбцов, называют разрешающим и выделяют кружком. За ведущий столбец выберем столбец, соответствующий переменной х2, т.к. сравнивания по модулю [-5] >[-3]; [-4]. Вычислим значения Разрешающий элемент равен 0,2 и находится на пересечении ведущего столбца и ведущей строки. 4. Построение нового плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала заменим переменные в базисе, т.е. вместо (х i) (х4) в базис войдет переменная (х j) (х2) соответствующая ведущему столбцу. 1. Разделим все элементы ведущей строки предыдущей симплексной таблицы на разрешающий элемент и результаты деления занесем в начальную строку следующей симплексной таблицы, т.е. (х2) 1100/0,2=5500; 0,1/0,2=0,5; 0,2/0,2=1;0,4/0,2=2;1/0,2=5. 2. Все остальные других строк определяются по формуле: нов.коэфф.=соотв.коэфф.пред.табл. – (коэфф.ведущ.столбца х коэфф.нач.строки нов. плана) Выполняя последовательно все этапы алгоритма, составляем план 2:
Анализ второго плана: План не оптимальный т.к. в индексной строке имеется отрицательный коэффициент (-0,5). Максимальный доход в размере 25.500 руб. торговое предприятие получит от продажи товаров второй группы В 5500 ед. (х2). Среди базисных переменных находится дополнительные переменные х5и х6. Это указывает на то, что ресурсы второго вида (площадь торговых залов) недоиспользована на 10 м2 и ресурсы третьего вида (площадь складских помещений) недоиспользованы на 2500 м2 . На третьей итерации получаем план 3, который является оптимальным т.к. все коэффициенты в индексной строке
Анализ третьего плана: Необходимо продавать товаров первой группы А 250 ед., а второй группы В 5375 ед. При этом торговое предприятие получает максимальный доход в размере 27625 тыс. руб. Товары группы С не реализуются. В оптимальном плане среди базисных переменных находится дополнительная переменная х6. Это указывает, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м2, т.к. переменная х6 была введена в третье ограничение задачи, характеризующее собой использование складских помещений этого ресурса.
|

 вi
вi  0 (i = 1, 2, …..m). Известны расходы ресурсов каждого i –го вида на реализацию единицы товара по каждой группе, представленной в виде матрицы А=(а ij), и прибыль “C j ”, получаемая предприятием от реализации единицы товара “j” группы. Надо определить объем и структуру товарооборота “хj” (j = 1, 2, …,n), при которых прибыль коммерческого предприятия была бы максимальной.
0 (i = 1, 2, …..m). Известны расходы ресурсов каждого i –го вида на реализацию единицы товара по каждой группе, представленной в виде матрицы А=(а ij), и прибыль “C j ”, получаемая предприятием от реализации единицы товара “j” группы. Надо определить объем и структуру товарооборота “хj” (j = 1, 2, …,n), при которых прибыль коммерческого предприятия была бы максимальной.
 a ij * хj
a ij * хj 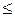 вi, i = 1,2 …m (1)
вi, i = 1,2 …m (1) mах (3)
mах (3) 0,1х1+0,2х2+0,4х3 + х4 = 1100
0,1х1+0,2х2+0,4х3 + х4 = 1100

 х4 = 1100 – (0,1х1+0,2х2+0,4х3)
х4 = 1100 – (0,1х1+0,2х2+0,4х3) i
i
 i
i 


