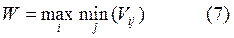Основы теории принятия решений в условиях неопределенности и риска
В условиях неопределенности (недостатка информации) внешняя среда («природа») может находиться в одном из множества конечных состояний. Поэтому принятие решений в условиях неопределенности часто называют «игры с природой». Пусть Si – состояние природы, которое меняется m раз (от 1 до m). Все состояния известны. Неизвестно только какое состояние будет иметь место в условиях, когда планируется реализация управленческого решения. Будем считать, что множество управленческих решений (планов) Rj – конечно и равняется n. Реализация плана Rj когда природа находится в состоянии Si приводит к одному из следственных результатов: 1. Выигрышу от принимаемого решения (плана); 2. Потерям; 3. Риску. Исходные данные для таких задач задаются в виде матрицы, строки которой соответствуют управленческим решением Rj, а столбцы - состояниям природы Si. Vij – результат (выигрыши или проигрыши). В качестве результатов в отдельных задачах используется матрица рисков. Риск – это мера несоответствия между разными возможными рультатами от принятия решений. Элементы матрицы рисков связаны с элементами матрицы выигрышей следующим соответствием: rij = max {Vij} - Vij, если Vij – выигрыш (6) где rij – элемент матрицы рисков Vij – элемент матрицы выигрышей. Если матрица результатов Vij представляет собой матрицу потерь, то элементы матрицы рисков rij рассчитывается следующим образом: rij = Vij - min {Vij}, если Vij – потери (7) Для принятия решений в условиях неопределенности используют критерии Лапласа, Вальда, Севиджа, Гурвица. Критерий Лапласа предполагает все состояния природы равновероятными, т.е. каждому состоянию Si ставится вероятность qi, определяемая по формуле: qi = где n - количество состояний природы Si При этом выбирается действие, дающее наибольший ожидаемый выигрыш:
где W –значения критерия Лапласа. Оптимальная стратегия выбирается по максимальному значению W. Если в исходной задаче дана матрица рисков rij, то оптимальную стратегию выбирают по минимальному значению W.
Пример. Транспортное предприятие должно определить уровень своих провозных возможностей, так чтобы удовлетворить спрос на транспортные услуги. Спрос точно не известен, но прогнозируется, что он может принимать 1 из 4-х значений. Для каждого уровня спроса существует наилучший уровень провозных возможностей, отклонение от которых проводят к дополнительным затратам. Определить оптимальный вариант провозных возможностей по данным следующей таблицы:
Применим критерий Лапласа Vij – матрица потерь
qi = W1 = 0,25(6+12+20+24)=15,6 W2 = 0,25(9+7+9+28)=13,25 W3 = 0,25(23+18+15+19) =18,75 W4 = 0,25(27+24+21+15)=21,75 Так как дана матрица потерь, то выбираем W с наименьшим значением. Т.о. наилучшая стратегия развития провозимых возможностей 2. Критерий Вальда. Если в исходной матрице результат Vij представляет собой потери, то при выборе оптимальной стратегии используют минимаксный критерий:
Если Vij элементы матрицы выигрышей, то используемых максиминный критерий:
Пример 4. Используя условия примера 3 выбрать оптимальную стратегию с помощью критерия Вальда. max (6; 12; 20; 24) =24 max (9; 7; 9; 28) =28 max (23; 18; 15; 19) =23 max (27; 24; 21; 15) =27 W = min (24; 28; 23; 27) =23 В соответствии с критерием Вальда наилучшей стратегий будет 3. Критерий Севиджа. Используется только для матрицы рисков, поэтому если даны матрицы выигрышей или потерь, то их необходимо пересчитать в матрицу рисков по формулам (6) или (7). Пример 5. Для исходных данных примера 3 применим критерий Севиджа. Рассчитаем матрицу рисков:
|

 ,
,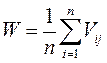 ,
, R1 V= R2
R3
R4
R1 V= R2
R3
R4
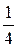 = 0,25
= 0,25