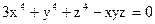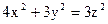Задания для контрольной работы .
Задание 1. Найти предел функции, не пользуясь правилом Лопиталя.
1.1. а) 1.2. а) 1.3. а) 1.4. а) 1.5. а) 1.6. а) 1.7. а) 1.8. а) 1.9. а) 1.10. а) 1.11. а) 1.12. а) 1.13. а) 1.14. а) 1.15. а) 1.16. а) 1.17. а) 1.18. а) 1.19. а) 1.20. а) 1.21 а) в) 1.22 а) в) 1.23 а) в) 1.24 а) в)
Задание 2. Найти производные указанных функций. 2.1. а) 2.2. а) 2.3. а) 2.4. а) 2.5. а) 2.6. а) 2.7. а) 2.8. а) 2.9. а) 2.10. а) 2.11. а) 2.12. а) 2.13. а) 2.14. а) 2.15 а) 2.16. а) 2.17. а) 2.18. а) 2.19. а) 2.20. а) 2.21 а) 2.22 а) 2.23 а) 2.24 а)
Задание 3. Найти
3.1. а) 3.2. а) 3.3. а) 3.4. а) 3.5. а) 3.6. а) 3.7. а) 3.8. а) 3.9. а) 3.10. а) 3.11. а) 3.12. а) 3.13. а) 3.14. а) 3.15. а) 3.16. а) 3.17. а) 3.18. а) 3.19. а) 3.20. а) 3.21 а) 3.22 а) 3.23 а) 3.24 а)
Задание 4. Дана функция
Задание 5. Найти производные указанного порядка функции, заданной неявно
ЛИТЕРАТУРА:
1. Зимина О.В. Линейная алгебра и аналитическая геометрия: Учебное пособие для студентов вузов. – М.: Издательство МЭИ, 2000.
2. Шипачев В.С. Высшая математика: Учебник для вузов. – 5-е издание. – М.: Высшая школа, 2002.
Для заметок
*) – укажите свойства определяемого понятия
|

 б)
б) 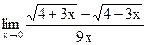
 г)
г) 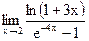
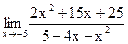 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
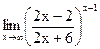 г)
г) 
 б)
б) 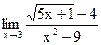
 г)
г) 
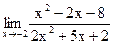 б)
б) 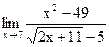
 г)
г) 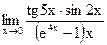
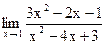 б)
б) 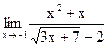
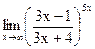 г)
г) 
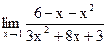 б)
б) 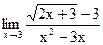
 г)
г) 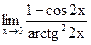
 б)
б) 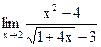
 г)
г) 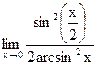
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
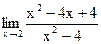 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
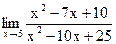 б)
б) 
 г)
г) 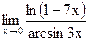
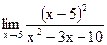 б)
б) 
 г)
г) 
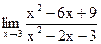 б)
б) 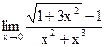
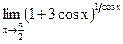 г)
г) 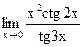
 б)
б) 
 г)
г) 
 б)
б) 
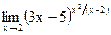 г)
г) 
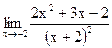 б)
б) 
 г)
г) 
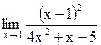 б)
б) 
 г)
г) 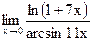
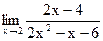 б)
б) 
 г)
г) 
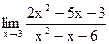 б)
б) 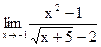
 г)
г) 
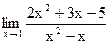 б)
б) 
 г)
г) 
 б)
б) 
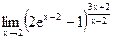 г)
г)  ,0
,0 б)
б)  в)
в) 
 б)
б)  в)
в) 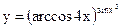
 б)
б)  в)
в) 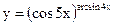
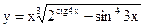 б)
б)  в)
в) 
 б)
б) 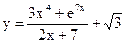 в)
в) 
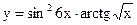 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б) 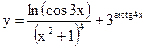 в)
в) 
 б)
б) 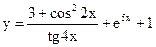 в)
в) 
 б)
б)  в)
в) 
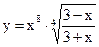 б)
б)  в)
в) 
 б)
б)  в)
в) 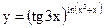
 б)
б) 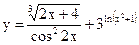 в)
в) 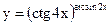
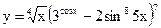 б)
б)  в)
в) 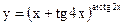
 б)
б) 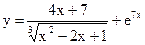 в)
в) 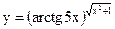
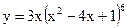 б)
б)  в)
в) 
 б)
б)  в)
в) 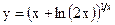
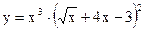 б)
б) 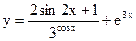 в)
в) 
 б)
б)  в)
в) 
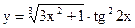 б)
б)  в)
в) 
 б)
б)  в)
в) 
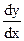 и
и 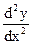 .
. б)
б) 
 б)
б) 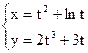
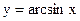 б)
б) 
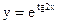 б)
б) 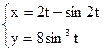
 б)
б) 
 б)
б) 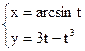
 б)
б) 
 б)
б) 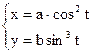
 б)
б) 
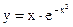 б)
б) 
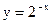 б)
б) 
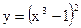 б)
б) 
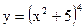 б)
б) 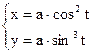
 б)
б) 
 б)
б) 
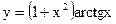 б)
б) 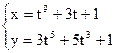
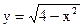 б)
б) 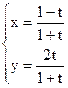
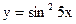 б)
б) 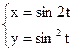
 б)
б) 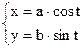
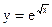 б)
б) 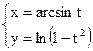
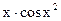 б)
б) 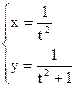
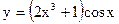 б)
б) 
 б)
б) 
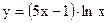 б)
б) 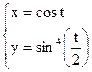
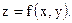 Показать, что она является решением дифференциального уравнения.
Показать, что она является решением дифференциального уравнения. ;
;

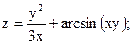


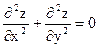
 ;
;

 ;
;

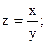
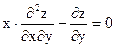



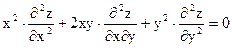

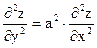

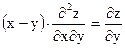
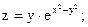

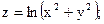

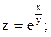

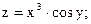
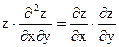
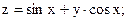

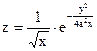 ;
;

 ;
;

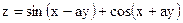 ;
;

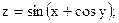


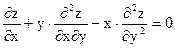
 ;
;

 ;
;
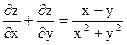
 ;
;
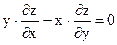

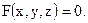

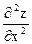

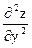

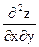
 ;
;

 ;
;
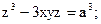



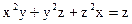 ;
;
 ;
;
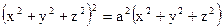 ;
;
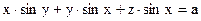 ;
;
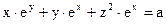 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;