IV. Функции нескольких переменных
1. Что называют функцией двух переменных, ее областью определения? Дайте геометрическое толкование этих понятий. 2. Дайте определение функции 3-х переменных и ее области определения. 3. Что называют пределом функции двух переменных в точке? Дайте определение функции, непрерывной в точке и в области. 4. Как определяются частные производные? Сформулируйте правило нахождения частных производных. Каков геометрический смысл частных производных функции двух переменных? 5. Какая функция 6. Выведите уравнение касательной плоскости и нормали к поверхности. 7. Выведите формулы для нахождения 8. Напишите формулу вычисления полной производной 9. Выведите формулу дифференцирования неявной функции 10. Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных частных производных функции двух переменных. 11. Что называют производной функции 12. Что называют градиентом скалярного поля 13. Дайте определение локального максимума (минимума) функции двух переменных. Выведите необходимое условие и сформулируйте достаточное условие экстремума функции двух переменных. 14. Сформулируйте правило нахождения наибольшего и наименьшего значений функции двух переменных в замкнутой области. 15. Что называют условным экстремумом функции 16. Напишите уравнение касательной и нормальной плоскости к кривой. 17. Как вычислить кривизну кривой в данной точке?
|

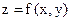 называется дифференцируемой в точке Мо(хо, уо)? Что называют полным дифференциалом функции в точке? В чем состоит правило применения полного дифференциала для вычисления приближенных значений функции?
называется дифференцируемой в точке Мо(хо, уо)? Что называют полным дифференциалом функции в точке? В чем состоит правило применения полного дифференциала для вычисления приближенных значений функции?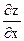 и
и 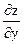 сложной функции
сложной функции  , где
, где  .
. ,
, 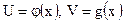 .
.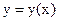 , заданной уравнением
, заданной уравнением  .
.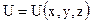 в данной точке М0 по направлению вектора? Выведите формулу ее вычисления.
в данной точке М0 по направлению вектора? Выведите формулу ее вычисления.


