Теплообмен в жидкостях и газах.
2.1.1. Теплоотдача при свободной конвекции Свободным называется движение подвижной среды вследствие разности плотностей нагретых и холодных частиц. Например, при соприкосновении воздуха с нагретым телом воздух нагревается, становится легче и поднимается вверх. При свободном движении жидкости в пограничном слое температура жидкости изменяется от Вначале толщина нагретого слоя мала и течение жидкости имеет струйчатый, ламинарный характер. Но по направлению движения толщина слоя увеличивается, и при определенном ее значении течение жидкости становится неустойчивым, волновым, локонообразным и затем переходит в неупорядоченно-вихревое, турбулентное, с отрывом вихрей от стенки. С изменением характера движения изменяется и теплоотдача. При ламинарном движении вследствие увеличения толщины пограничного слоя коэффициент теплоотдачи В развитии свободного движения форма тела играет второстепенную роль. Здесь большее значение имеют протяженность поверхности, вдоль которой происходит движение, и ее положение. Описанная выше картина движения жидкости вдоль плоской вертикальной стенки (или вдоль вертикальной трубы) типична также и для горизонтальных труб и тел овальной формы. При изучении интенсивности теплообмена в условиях свободного движения были проведены исследования с разными телами и различными жидкостями. В результате обобщения опытных данных получены критериальные зависимости для средних значений коэффициента теплоотдачи.
В этих формулах в качестве определяющей температуры принята температура окружающей среда Закономерность средней теплоотдачи для горизонтальных труб диаметром
где По вычисленному значению коэффициента Nu определяют коэффициент теплоотдачи
Плотность теплового поток с поверхности тела определится по формуле
Закономерность средней теплоотдачи для вертикальных поверхностей (трубы, пластины) следующая а) при
б) при
где По вычисленному значению коэффициента Nu определяют коэффициент теплоотдачи
Индексы «ж» и «с» означают, что физические свойства жидкости выбираются по средней температуре жидкости и стенки соответственно. Множитель
2.1.2. Теплоотдача при поперечном обтекании цилиндрического стержня.
Процесс теплоотдачи при поперечном обтекании цилиндрического стержня (трубы, кабеля) имеет ряд особенностей, которые объясняются гидродинамической картиной движения жидкости вблизи поверхности трубы. Опыт показывает, что плавный, безотрывной характер обтекания трубы имеет место только при очень малых числах Рейнольдса
Рис. 2.3. Обтекание одиночного цилиндра. а – безотрывное (ламинарное); б – с образованием вихря в кормовой зоне
Сложный характер обтекания цилиндра существенно затрудняет теоретическое исследование закономерностей теплообмена. Поэтому основным методом изучения теплоотдачи при поперечном обтекании труб является эксперимент. Опыт показывает, что коэффициент теплоотдачи В результате анализа и обобщения существующих экспериментальных данных для расчета среднего по периметру трубы коэффициент теплоотдачи, можно определить по формулам при
при
где
По вычисленному значению коэффициента Nu определяют коэффициент теплоотдачи
Эти соотношения справедливы лишь тогда, когда угол
Рис. 2.4. Зависимость теплоотдачи цилиндра от угла атаки потока жидкости
|

 до
до  , а скорость – от нуля у стенки, проходит через максимум и на большом удалении от стенки снова равна нулю (рис. 2.1).
, а скорость – от нуля у стенки, проходит через максимум и на большом удалении от стенки снова равна нулю (рис. 2.1). по направлению движения убывает, а при турбулентном – он резко возрастает и затем по высоте остается постоянным (рис. 2.2).
по направлению движения убывает, а при турбулентном – он резко возрастает и затем по высоте остается постоянным (рис. 2.2).

 при свободном движении вдоль нагретой вертикальной поверхности
при свободном движении вдоль нагретой вертикальной поверхности
 , а для вертикальных поверхностей – высота
, а для вертикальных поверхностей – высота  .
.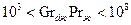 имеет вид
имеет вид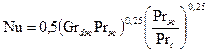 , (2.1)
, (2.1) ;
; 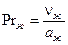 ;
;  .
. . (2.2)
. (2.2) , (2.3)
, (2.3) (ламинарный режим)
(ламинарный режим) , (2.4)
, (2.4) (турбулентный режим)
(турбулентный режим) , (2.5)
, (2.5) .
. . (2.6)
. (2.6) , входящий в формулу, представляет собой поправку, учитывающую влияние изменения физических параметров теплоносителя с изменение температуры на теплоотдачу.
, входящий в формулу, представляет собой поправку, учитывающую влияние изменения физических параметров теплоносителя с изменение температуры на теплоотдачу. . При значительно больших числах Рейнольдса
. При значительно больших числах Рейнольдса  , характерных для практики обтекания трубы всегда сопровождается образованием в кормовой части вихревой зоны, как это показано на рис 3. Здесь
, характерных для практики обтекания трубы всегда сопровождается образованием в кормовой части вихревой зоны, как это показано на рис 3. Здесь  – скорость невозмущенного потока жидкости.
– скорость невозмущенного потока жидкости.
 в наибольшей мере зависит от скорости набегающего потока, плотности и теплопроводности и в меньшей степени от теплоемкости и вязкости жидкости. Кроме того, коэффициент теплоотдачи
в наибольшей мере зависит от скорости набегающего потока, плотности и теплопроводности и в меньшей степени от теплоемкости и вязкости жидкости. Кроме того, коэффициент теплоотдачи 
 , (2.7)
, (2.7)
 , (2.8)
, (2.8) .
.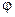 , составленный направлением движения потока и осью трубы, равен
, составленный направлением движения потока и осью трубы, равен 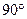 . Зависимость теплоотдачи от величины угла атаки представлены на рис. 2.4. По оси абсцисс отложен угол
. Зависимость теплоотдачи от величины угла атаки представлены на рис. 2.4. По оси абсцисс отложен угол 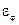 , которое представляет собой отношение теплоотдачи при угле атаки
, которое представляет собой отношение теплоотдачи при угле атаки 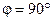 , т.е.
, т.е.  . Как видно из рис. 2.4 с уменьшением угла атаки, значение
. Как видно из рис. 2.4 с уменьшением угла атаки, значение  .
.  по следующей приближенной формуле
по следующей приближенной формуле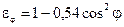 .
.



