Рассмотренный ранее метод можно использовать только в том случае, ели все ограничения являются неравенствами типа ≤ с неотрицательными правыми частями. Во всех других случаях шаг нахождения начального допустимого базисного решения не такой простой.
Самый простой способ получения начального допустимого базисного решения – это использование искусственных переменных.
Пусть задача ЛП записана в канонической форме. Для любого равенства, в котором не содержится дополнительная переменная с коэффициентом 1, введем искусственную переменную  , которая далее войдет в начальное базисное решение. Но поскольку эта переменная искусственна, необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
, которая далее войдет в начальное базисное решение. Но поскольку эта переменная искусственна, необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная  с помощью достаточно большого положительного числа
с помощью достаточно большого положительного числа  штрафуется путем ввода в целевую функцию выражения
штрафуется путем ввода в целевую функцию выражения 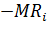 в случае максимизации и
в случае максимизации и  в случае минимизации. Этот штраф предназначен для того, чтобы в процессе оптимизации переменные
в случае минимизации. Этот штраф предназначен для того, чтобы в процессе оптимизации переменные  обратились в нуль.
обратились в нуль.
После ввода искусственных переменных можно переходить к построению первоначальной симплекс таблицы. Однако следует обратить внимание на следующее: ввод в целевую функцию штрафов приведет к тому, что значение целевой функции  в начальном базисном решении не будет равно нулю. Поэтому необходимо выполнить согласование -строки с остальной частью таблицы. Для этого в выражение целевой функции необходимо подставить значение базисных переменных и определить чему равно
в начальном базисном решении не будет равно нулю. Поэтому необходимо выполнить согласование -строки с остальной частью таблицы. Для этого в выражение целевой функции необходимо подставить значение базисных переменных и определить чему равно  . Затем необходимо пересчитать коэффициенты -строки так, чтобы значение
. Затем необходимо пересчитать коэффициенты -строки так, чтобы значение  соответствовало вычисленному. Новый коэффициент в -строке будет равен старому плюс сумма произведений коэффициентов в остальных строках умноженных на коэффициенты при соответствующих переменных в целевой функции.
соответствовало вычисленному. Новый коэффициент в -строке будет равен старому плюс сумма произведений коэффициентов в остальных строках умноженных на коэффициенты при соответствующих переменных в целевой функции.
После согласования переходим к 3-му шагу алгоритма обычного симплекс-метода.

 , которая далее войдет в начальное базисное решение. Но поскольку эта переменная искусственна, необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
, которая далее войдет в начальное базисное решение. Но поскольку эта переменная искусственна, необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф. штрафуется путем ввода в целевую функцию выражения
штрафуется путем ввода в целевую функцию выражения 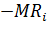 в случае максимизации и
в случае максимизации и  в случае минимизации. Этот штраф предназначен для того, чтобы в процессе оптимизации переменные
в случае минимизации. Этот штраф предназначен для того, чтобы в процессе оптимизации переменные  в начальном базисном решении не будет равно нулю. Поэтому необходимо выполнить согласование -строки с остальной частью таблицы. Для этого в выражение целевой функции необходимо подставить значение базисных переменных и определить чему равно
в начальном базисном решении не будет равно нулю. Поэтому необходимо выполнить согласование -строки с остальной частью таблицы. Для этого в выражение целевой функции необходимо подставить значение базисных переменных и определить чему равно 


