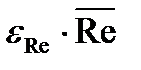Статистическая обработка результатов измерений
1. Рассчитайте средние значения диаметра и массы шариков, после чего вычислите среднюю плотность материала шарика
где 2. Рассчитайте среднее значение коэффициента динамической вязкости
где 3. Вычислите абсолютную погрешность измерения коэффициента динамической вязкости. Для этого 3.1. Найдите случайные погрешности прямых измерений диаметра шарика d, длины пути l и времени падения шарика t при доверительной вероятности 0.95
3.2. Найдите абсолютные погрешности измерения диаметра шарика d, длины пути l и времени падения шарика t
где 3.3. Рассчитайте относительную погрешность косвенных измерений коэффициента вязкости
3.4. Искомая абсолютная погрешность измерения коэффициента вязкости равна
4. Рассчитайте среднее значение числа Рейнольдса
5. Вычислите абсолютную погрешность косвенных измерений числа Рейнольдса ΔRe Для этого 5.1. Рассчитайте относительную погрешность косвенных измерений числа Рейнольдса, выразив его через прямо измеренные величины: поскольку
5.2. Искомая абсолютная погрешность числа Рейнольдса равна
|
,
- средняя масса шариков; 
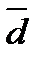- средний диаметр шариков. Результаты занесите в соответствующие ячейки 4 строки таблицы
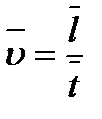средняя скорость движения шариков.
,
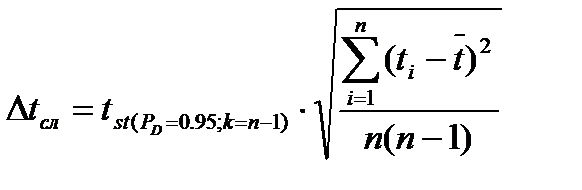
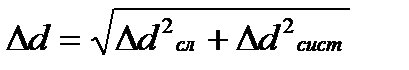
Δdсист., Δlсист., Δtсист – систематические погрешности измерений.
.
= 
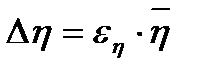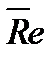
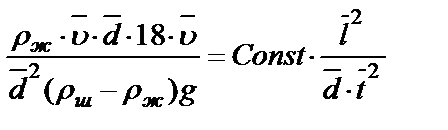, относительная погрешность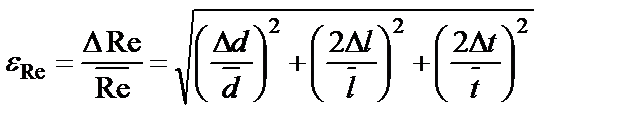
=. 
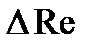