Расчетная часть. Сила связи Направление связи Прямая (+) Обратная (-) Сильная от + 1 до + 0,7 от -1 до - 0,7 Средняя
Линейный закон изменения диагностических параметров
Цель работы: Подобрать коэффициенты а и b линейной зависимости по методу наименьших квадратов Теоретическая часть Аппроксимация экспериментальных данных линейными зависимостями, см. рис. 1. y = ax + b (1)
Рисунок 1 - Аппроксимация экспериментальных данных линейными зависимостями.
Запишем выражения экспериментальных отклонений данных от выбранного направления:
Теперь суммируем квадраты полученных отклонений:
Возьмем частные производные от выражения (3)
Для нахождения значений коэффициентов, соответствующих минимальной сумме квадратов полученных отклонений приравняем полученные частные производные к нулю. Раскроем скобки – получим систему линейных уравнений
Определим коэффициенты а и b, решив систему уравнений по правилу Крамера:
Запишем уравнение аппроксимирующей прямой:
Расчетная часть Экспериментальные значения параметра Р (силы тяги на колёсах) автомобиля ГАЗ 3102 представлены в табл.1
Таблица 1 - Cилы тяги на колёсах автомобиля ГАЗ 3102
Определим коэффициенты а и b, используя формулы (2.7) - (2.11). Полученные результаты занесем в табл. 2.2.
Таблица 2 - Коэффициенты
Запишем уравнение аппроксимирующей прямой:
Построим график экспериментальных данных Р(x) и аппроксимирующую прямую.
Рисунок 2 - График экспериментальных данных Р(x) и аппроксимирующая прямая Рт(x). Вывод В результате обработки экспериментальных данных с помощью метода наименьших квадратов определены значения коэффициентов а = и b = и получено уравнение аппроксимирующей прямой
Корреля́ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции R. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин. Линейный коэффициент корреляции R (или коэффициент корреляции Пирсона) рассчитывается по формуле:
где Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы.
|


 (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)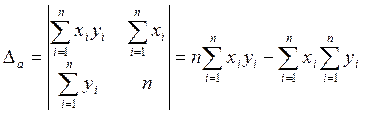 (8)
(8)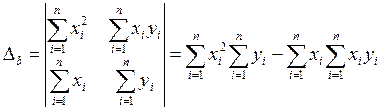 (9)
(9) (10)
(10)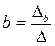 (11)
(11)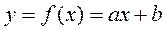 (12)
(12) км
км











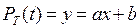
 ,
, ,
, 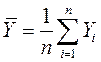 — средние значения выборок.
— средние значения выборок.


