Подналадка по положению центра группирования
В отличие от предыдущего метода здесь текущее значение Подналадка реализуется следующим образом. Детали сходящие с рабочей позиции автомата, контролируются N датчиками (рис.5.4) причем каждая деталь последовательно проходит все датчики, настроенные на установку
Рис. 5.4. Схема подналадки по положению центра группирования
Если используется метод среднего арифметического, то отклонения алгебраически складываются в сумматоре. Когда их сумма станет равной нулю, срабатывает система автоподналадки и перестраивает оборудование. Если используется метод медианы, то отклонения необходимо суммировать с определенными весами. Однако на практике используют упрощенный метод: контролируется только знак и число отклонений Для срабатывания системы автоподналадки достаточно, чтобы число положительных отклонений от Найдем оценку В связи с тем, что систематическая составляющая погрешности При этом для
Проверка состоятельности и несмещенности оценки
В полученном выражении второе слагаемое представляет собой сумму арифметической прогрессии и его модуль равен четвертому слагаемому, третье же слагаемое равно нулю. В результате имеем:
Таким образом, оценка является состоятельной и несмещенной. Определим дисперсию оценки. В соотношении (5.8) три слагаемых являются постоянными и их дисперсии равны нулю. Поэтому дисперсия оценки
Величина зоны подналадки
Рис. 5.5. К определению доверительного интервала
Для определения длины доверительного интервала учтем, что оценка В этом случае для определения
где Так как разница между оценкой и оцениваемой величиной в выражении (11) берется по абсолютной величине, то величина зоны подналадки с заданной вероятностью
На практике обычно N = 4…6. Использование упрощенного метода медианы дает большее значение зоны подналадки
Однако эта разновидность метода менее чувствительна к грубым ошибкам, в то время как оценка Но при выборе установки следует учесть, что до сих пор рассматривались абсолютные значения оценки, в то время как метод реализуется с использованием отклонений от уставки. Поэтому для правильного расположения зоны подналадки уставка должна быть выбрана в соответствии с рис. 5.6.
Рис. 5.6. Структура суммарной погрешности обработки при наладке по центру группирования
Суммарная погрешность рассмотренного метода имеет ту же структуру, что и погрешность подналадки по одной детали. Поэтому можно использовать формулы (5.4), (5.5), (5.6), подставляя в них вместо
|

 определяют по выборке из N деталей. В данном методе различают подналадку по среднему арифметическому значению и подналадку по медиане.
определяют по выборке из N деталей. В данном методе различают подналадку по среднему арифметическому значению и подналадку по медиане. . Датчики контролируют величину и знак отклонения параметра соответствующей детали от
. Датчики контролируют величину и знак отклонения параметра соответствующей детали от 
 ,
,  , …,
, …, 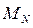 .
.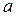 ,
,  ,т.е.
,т.е.  ,где
,где  - центрированная случайная величина, подчиняющаяся нормальному закону распределения с дисперсией
- центрированная случайная величина, подчиняющаяся нормальному закону распределения с дисперсией  .
. , (5.7)
, (5.7) сводится к определению ее математического ожидания
сводится к определению ее математического ожидания . (5.8)
. (5.8) . (5.9)
. (5.9) . (5.10)
. (5.10) в этом случае будет определяться доверительным интервалом
в этом случае будет определяться доверительным интервалом  с центром в точке
с центром в точке 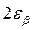 , который накроет точку
, который накроет точку  c вероятностью
c вероятностью 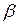 т.е.
т.е. . (5.11)
. (5.11)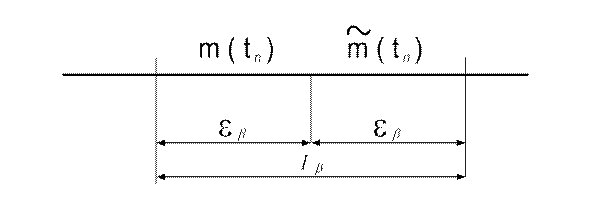
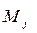 и, следовательно, сама является случайной величиной, распределенной по нормальному закону с математическим ожиданием (5.9) и дисперсией (5.10).
и, следовательно, сама является случайной величиной, распределенной по нормальному закону с математическим ожиданием (5.9) и дисперсией (5.10). можно использовать функцию Лапласа [3]
можно использовать функцию Лапласа [3] . Откуда длина доверительного интервала выразится соотношением
. Откуда длина доверительного интервала выразится соотношением ,
, - квантиль нормального распределения, т.е. такое значение аргумента, для которого функция Лапласа равна
- квантиль нормального распределения, т.е. такое значение аргумента, для которого функция Лапласа равна  ,
, 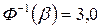 .
. .
. .
.
 величины (5.12), (5.13), а вместо погрешности контрольного устройства
величины (5.12), (5.13), а вместо погрешности контрольного устройства  или
или  .
.


