Процесс подналадки в соответствии с данным методом реализуется следующим образом. Предельный датчик настроенный на уставку  ,последовательно контролирует все детали, сходящие с рабочей позиции автомата. Если величина параметра
,последовательно контролирует все детали, сходящие с рабочей позиции автомата. Если величина параметра 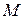 какой-либо детали превысит величину
какой-либо детали превысит величину  ,то система перестраивается на величину подналадочного импульса A.
,то система перестраивается на величину подналадочного импульса A.
Оценим точные характеристики метода. Как следует из рис. 5.2, вероятность подналадки  возникает практически при контроле
возникает практически при контроле  - й детали, если пренебречь вероятностью меньшей 0,00134. Центр группирования
- й детали, если пренебречь вероятностью меньшей 0,00134. Центр группирования  в этот момент определяет положение нижней границы
в этот момент определяет положение нижней границы  зоны подналадки
зоны подналадки  . Так как события подналадки и неподналадки являются противоположными, то вероятность неподналадки в момент времени
. Так как события подналадки и неподналадки являются противоположными, то вероятность неподналадки в момент времени  равна
равна
 ,
,
где  - номер детали;
- номер детали;  - часть площади
- часть площади 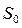 дифференциального закона распределения отсекаемая на уровне
дифференциального закона распределения отсекаемая на уровне  .
.
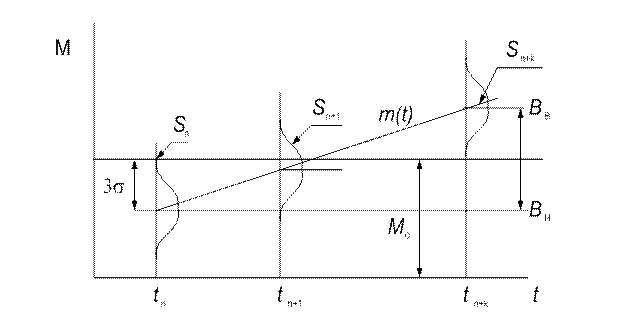
Рис. 5.2. К определению вероятности подналадки по одной детали
Если подналадка в момент  не произойдет, то вероятность неподналадок в моменты времени
не произойдет, то вероятность неподналадок в моменты времени 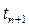 ,
, 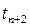 , …,
, …,  можно определить как вероятности сложных событий, используя закон умножения независимых вероятностей. Тогда вероятность неподналадки в момент времени
можно определить как вероятности сложных событий, используя закон умножения независимых вероятностей. Тогда вероятность неподналадки в момент времени  можно выразить следующим образом
можно выразить следующим образом
 . (5.1)
. (5.1)
Как следует из выражения (1), вероятность неподналадки при увеличении 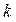 уменьшается. Поэтому определив
уменьшается. Поэтому определив 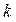 , начиная с которого вероятность неподналадки практически равна нулю
, начиная с которого вероятность неподналадки практически равна нулю  ,а вероятность подналадки
,а вероятность подналадки  ,можно установить положение верхней границы
,можно установить положение верхней границы 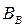 зоны подналадки
зоны подналадки  .
.
Если предположить, что систематическая составляющая погрешности изменяется линейно, причем величина изменения ее за время изготовления одной детали равна  , то ширина зоны
, то ширина зоны
 (5.2)
(5.2)
Таким образом, зная величину приращения 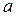 и определив по формуле (5.1) значение
и определив по формуле (5.1) значение 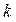 , можно вычислить ширину зоны подналадки
, можно вычислить ширину зоны подналадки  .
.
Величины отношений  можно определить по интегралу вероятностей
можно определить по интегралу вероятностей  табулированные значения которого приведены на лабораторном макете
табулированные значения которого приведены на лабораторном макете
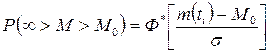 .
.
Пример. Дано:  . Определить ширину зоны подналадки
. Определить ширину зоны подналадки  . Практически вероятность подналадки возникает при
. Практически вероятность подналадки возникает при  , т.е.
, т.е. 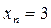 . Тогда
. Тогда 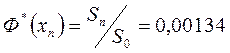 . Рассчитывая последовательно значения
. Рассчитывая последовательно значения  ,
,  , …,
, …,  в соответствии с соотношением (1) вычислим вероятность неподналадки для разных
в соответствии с соотношением (1) вычислим вероятность неподналадки для разных 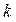
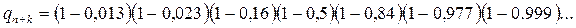
Получим, что 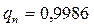 ,
,  ,
,  ,
,  ,
, 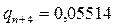 ,
, 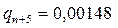 ,
, 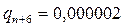 ,т.е. начиная с
,т.е. начиная с  , вероятность подналадки практически равна 1, а искомая величина зоны подналадки
, вероятность подналадки практически равна 1, а искомая величина зоны подналадки  .
.
При  такой способ определения зоны подналадки
такой способ определения зоны подналадки  становится трудоемким, так как с увеличением
становится трудоемким, так как с увеличением 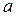 а растет
а растет 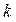 . Поэтому на практике используют приближенное значение
. Поэтому на практике используют приближенное значение
 (5.3)
(5.3)
где  ;
; 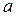 – выражается в единицах среднеквадратического отклонения
– выражается в единицах среднеквадратического отклонения  .
.
При указанных ранее ограничениях суммарное распределение выходного параметра 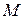 партии деталей будет представлять собой композицию законов Гаусса и равной вероятности
партии деталей будет представлять собой композицию законов Гаусса и равной вероятности 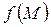 (рис.5.1).
(рис.5.1).
Величина подналадочного импульса  определяется положением зоны подналадки
определяется положением зоны подналадки  , полем допуска
, полем допуска  контролируемого параметра
контролируемого параметра  , величиной среднеквадратического отклонения
, величиной среднеквадратического отклонения  случайной составляющей погрешности и погрешностью измерительного прибора
случайной составляющей погрешности и погрешностью измерительного прибора  подналадочной системы
подналадочной системы  .
.
При большом количестве подналадок величина подналадочного импульса определяется по методу максимума-минимума (рис. 5.3)
 . (5.4)
. (5.4)
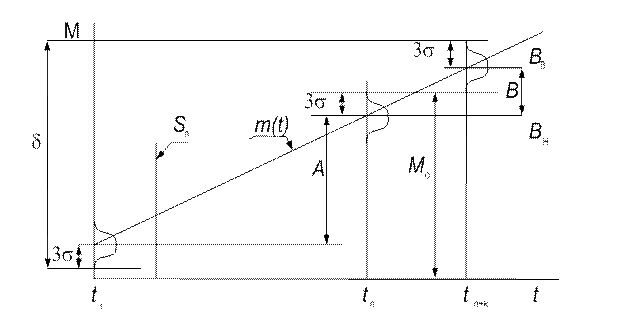
Рис. 5.3. Структура суммарной погрешности обработки при подналадке
по одной детали
При небольшом числе подналадок и малом значении параметра на практике используют квадратическое сложение случайных погрешностей. Причем последние имеют нормальные законы распределения
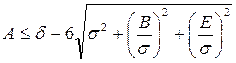 . (5.5)
. (5.5)
При небольшом числе подналадок и интенсивно изменяющейся систематической составляющей погрешности используют формулу квадратического сложения, но составляющая погрешности определения предельного значения 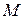 не имеет нормального закона. Поэтому:
не имеет нормального закона. Поэтому:
 , (5.6)
, (5.6)
где  – коэффициент, зависящий от формы распределения суммарной погрешности.
– коэффициент, зависящий от формы распределения суммарной погрешности.

 ,последовательно контролирует все детали, сходящие с рабочей позиции автомата. Если величина параметра
,последовательно контролирует все детали, сходящие с рабочей позиции автомата. Если величина параметра 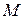 какой-либо детали превысит величину
какой-либо детали превысит величину  возникает практически при контроле
возникает практически при контроле  - й детали, если пренебречь вероятностью меньшей 0,00134. Центр группирования
- й детали, если пренебречь вероятностью меньшей 0,00134. Центр группирования  в этот момент определяет положение нижней границы
в этот момент определяет положение нижней границы  зоны подналадки
зоны подналадки  . Так как события подналадки и неподналадки являются противоположными, то вероятность неподналадки в момент времени
. Так как события подналадки и неподналадки являются противоположными, то вероятность неподналадки в момент времени  равна
равна ,
, - часть площади
- часть площади 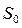 дифференциального закона распределения отсекаемая на уровне
дифференциального закона распределения отсекаемая на уровне 
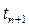 ,
, 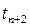 , …,
, …,  можно определить как вероятности сложных событий, используя закон умножения независимых вероятностей. Тогда вероятность неподналадки в момент времени
можно определить как вероятности сложных событий, используя закон умножения независимых вероятностей. Тогда вероятность неподналадки в момент времени  . (5.1)
. (5.1)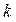 уменьшается. Поэтому определив
уменьшается. Поэтому определив  ,а вероятность подналадки
,а вероятность подналадки  ,можно установить положение верхней границы
,можно установить положение верхней границы 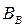 зоны подналадки
зоны подналадки  , то ширина зоны
, то ширина зоны (5.2)
(5.2)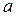 и определив по формуле (5.1) значение
и определив по формуле (5.1) значение  можно определить по интегралу вероятностей
можно определить по интегралу вероятностей  табулированные значения которого приведены на лабораторном макете
табулированные значения которого приведены на лабораторном макете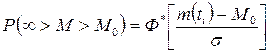 .
. . Определить ширину зоны подналадки
. Определить ширину зоны подналадки  , т.е.
, т.е. 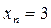 . Тогда
. Тогда 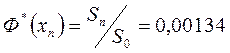 . Рассчитывая последовательно значения
. Рассчитывая последовательно значения  ,
,  , …,
, …,  в соответствии с соотношением (1) вычислим вероятность неподналадки для разных
в соответствии с соотношением (1) вычислим вероятность неподналадки для разных 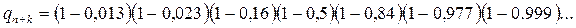
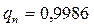 ,
,  ,
,  ,
,  ,
, 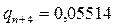 ,
, 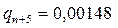 ,
, 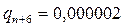 ,т.е. начиная с
,т.е. начиная с  , вероятность подналадки практически равна 1, а искомая величина зоны подналадки
, вероятность подналадки практически равна 1, а искомая величина зоны подналадки  .
. такой способ определения зоны подналадки
такой способ определения зоны подналадки  (5.3)
(5.3) .
.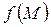 (рис.5.1).
(рис.5.1). определяется положением зоны подналадки
определяется положением зоны подналадки  подналадочной системы
подналадочной системы  .
. . (5.4)
. (5.4)
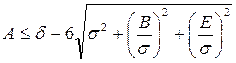 . (5.5)
. (5.5) , (5.6)
, (5.6) – коэффициент, зависящий от формы распределения суммарной погрешности.
– коэффициент, зависящий от формы распределения суммарной погрешности.


