Расчет однофазной разветвленной цепи переменного тока с помощью векторной диаграммы
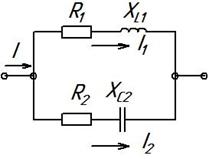
Цепь, состоящая из двух параллельных ветвей (рисунок 2.2), параметры которых: R1 = 16 Ом; ХL1 = 12 Ом; R2 = 30 Ом; ХС2 = 40 Ом присоединена к сети с напряжением U = 179 sin 628 t. Определить частоту электрической сети, действующее значение напряжения сети, токи в параллельных ветвях и ток в неразветвленной части, коэффициент мощности каждой ветви и всей цепи, углы сдвига фаз токов относительно напряжения сети, активную, реактивную и полную мощности цепи.
Рисунок 2.2 – Схема разветвленной цепи переменного тока
Частота электрической цепи определяется из формулы угловой частоты: ω = 2πf (2.12) Откуда,
Действующее значение напряжения определяется по известному амплитудному значению напряжения (Um):
Для определения токов необходимо найти проводимость ветвей и всей цепи: 1) активная, реактивная и полная проводимости первой ветви:
2) активная, реактивная и полная проводимости второй ветви:
3)
G = 0,04 + 0,012 = 0,052 См B = 0,03 + (– 0,016) = 0,014 См
Определяем токи в ветвях и ток в неразветвленной части цепи: I1 = U Y1 (2.23) I2 = U Y2 (2.24) I = U Y (2.25) I1 = 127×0,05 = 6,35 А; I2 = 127×0,02 = 2,54 А; I = 127×0,054 = 6,86 А. Определяем коэффициент мощности и углы сдвига фаз относительно напряжения каждой ветви и всей цепи:
cos φ1 = 0,04 / 0,05 = 0,8 φ1 = 370 cos φ2 = 0,012 / 0,02 =0,6 sin φ2 = - 0.8 φ2 = -530 cos φ = 0,052 / 0,054 = 0,963 φ = 120. По коэффициентам мощности cos φ с помощью таблиц Брадиса или инженерного калькулятора определяются углы сдвига фаз между токами и напряжениями. Определяем активную, реактивную и полную мощности цепи: Р = U2 G (2.29) Q = U2 B (2.30) S = U2 Y (2.31) Р = 1272 × 0,052 = 838,7 Вт Q =1272 × 0,014 = 225,8 вар S =1272 × 0,054 = 871 ВА
|


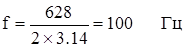
 (2.13)
(2.13)
 (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16)


 (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19)


 активная, реактивная и полная проводимости всей цепи:
активная, реактивная и полная проводимости всей цепи: (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22)
 (2.26)
(2.26) (2.27)
(2.27) 2.4 Построение векторной диаграммы разветвленной цепи
2.4 Построение векторной диаграммы разветвленной цепи


