Расчет однофазной разветвленной цепи переменного тока с помощью комплексных чисел
В электрической цепи, схема которой приведена на рисунке 2.3, действуют две синусоидальных ЭДС e1 = E1m sin (314t +Ψ1e) В и e2 = E2m sin (314t +Ψ2e). Параметры ЭДС и элементов схемы E1m = 537,4 В; Ψ1e = 00; E2m= 933,4 В; ХС2 = 6 Ом; R3 = 12 Ом; ХL3 = 20 Ом; ХС3 = 4 Ом. Определить токи в ветвях. Расчет вести методом двух узлов с применением комплексных чисел.
Рисунок 2.3 – Схема разветвленной цепи переменного тока с двумя узлами Задачу решаем символическим методом. Поэтому ее решение такое же, как при постоянном токе. Для решения необходимо представить сопротивления ветвей схемы в алгебраической и показательной формах записи комплексного числа: Z 1 = R1 + j (XL1 – XС1) (2.38) Z 2 = R2 + j (XL2 – XС2) (2.39) Z 3 = R3 + j (XL3 – XС3) (2.40) Z 1 = 3 + j (4 – 0) = 5 e j 53,1˚ Ом Z 2 = 8 + j (0 – 6) = 10 e – j 36,9˚ Ом Z 3 = 12 + j (20 – 4) = 20 e j 53,1˚ Ом Cхема приобретает вид (рисунок 2.4)
Рисунок 2.4 – Схема разветвленной цепи переменного тока в комплексном виде Обозначим на схемах направления токов ветвей İ1, İ2, İ3, произвольно выберем их направления к узлу 1. Определим действующие значения ЭДС:
Запишем значения ЭДС в показательной и алгебраической формах записи комплексного числа: Ė1 = E1e j Ψ1˚ (2.43) Ė2 = E2e j Ψ2˚ (2.44) Ė1 = 380 e j 0˚ = 380 + j0 В Ė2 = 660 e j 30˚ = 571,6 + j330 В Определяем проводимости ветвей в комплексной форме:
Определяем узловое напряжение
Определяем токи ветвей:
Проверим правильность решения по первому закону Кирхгофа: İ1+ İ2+ İ3 = 0 (– 3.7 – j41.0) + (16,0 + j36.0) + (– 12,3 + j5.0) = 0 Вывод: токи определены верно.
Определяем мощности источников по формулам:
где,
|

 Ψ2e = 300; R1 = 3 Ом; ХL1 = 4 Ом; ХС1 = 0; R2 = 8 Ом; ХL2 = 0;
Ψ2e = 300; R1 = 3 Ом; ХL1 = 4 Ом; ХС1 = 0; R2 = 8 Ом; ХL2 = 0;


 (2.41)
(2.41) (2.42)
(2.42)

 (2.45)
(2.45) (2.46)
(2.46) (2.47)
(2.47)


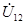 :
: (2.48)
(2.48)
 (2.49)
(2.49) (2.50)
(2.50) (2.51)
(2.51) 



 (2.52)
(2.52)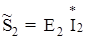 (2.53)
(2.53)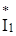 = 41.2 e j 95,1˚ А – вектор тока, сопряженный с током İ1 = 41.2 e – j 95,1˚ А
= 41.2 e j 95,1˚ А – вектор тока, сопряженный с током İ1 = 41.2 e – j 95,1˚ А = 39,5 e – j 65,3˚ А – вектор тока, сопряженный с током İ2 = 39,5 e j 65,3˚ А
= 39,5 e – j 65,3˚ А – вектор тока, сопряженный с током İ2 = 39,5 e j 65,3˚ А = 380 e j 0˚ × 41.2 e j 95,1˚ = 15656 e j 95,1˚ = – 1392 + j15594 ВА
= 380 e j 0˚ × 41.2 e j 95,1˚ = 15656 e j 95,1˚ = – 1392 + j15594 ВА = 660 e j 30˚ × 39,5 e – j 65,3˚ = 26070 e – j 35,3˚ = 21277 – j15065 ВА
= 660 e j 30˚ × 39,5 e – j 65,3˚ = 26070 e – j 35,3˚ = 21277 – j15065 ВА


