Упругие постоянные материала
Опытами установлено, что отношение относительной поперечной к относительной продольной деформации для каждого материала есть величина постоянная. Это отношение, взятое по абсолютной величине, называется коэффициентом поперечной деформации (коэффициентом Пуассона):
Коэффициент Пуассона Для различных материалов В упругой стадии работы большинства конструкционных материалов напряжения и деформации (например, при растяжении) связаны прямой пропорциональной зависимостью (рисунок 12): σ = Е ε;, (6) где Е – коэффициент пропорциональности.
Рисунок 12. Диаграмма растяжения низкоуглеродистой стали (участок пропорциональности)
Коэффициент Е называется модулем продольной упругости (модулем упругости при растяжении или модулем упругости I рода, модулем Юнга). Из графика (рисунок 12) и формулы (6) следует, что модуль продольной упругости определяется углом наклона α; прямой на участке ОА, т.е. отношением
Модуль упругости I рода есть вторая упругая постоянная материала и характеризует способность материала сопротивляться упругим деформациям растяжения или сжатия. Определяется опытным путем – испытанием образца, изготовленного из исследуемого материала. Имеет размерность напряжений. Впервые идею об этом модуле высказал в 1800 г. англичанин Томас Юнг, а современное толкование модуля дал в 1826 г. француз Луи Навье. В таблице 1 приводятся значения упругих постоянных для некоторых конструкционных и строительных материалов при нормальных условиях испытаний. Таблица 1 Упругие постоянные некоторых конструкционных и строительных материалов
Для изотропных материалов постоянные Е и Для анизотропных материалов (дерево, бумага, пластмасса и т.д.) эти величины для разных направлений измерения деформаций различны.
|


 . (5)
. (5)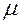 – всегда положительная безразмерная величина. Его величина определяется опытным путем для каждого материала и условий испытаний. Эту величину впервые теоретически получил француз Пуассон: для всех материалов – 0,25.
– всегда положительная безразмерная величина. Его величина определяется опытным путем для каждого материала и условий испытаний. Эту величину впервые теоретически получил француз Пуассон: для всех материалов – 0,25.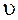 изменяется в пределах от 0 до 0,5. Для большинства металлов
изменяется в пределах от 0 до 0,5. Для большинства металлов  0,3 (для стали Ст. 3
0,3 (для стали Ст. 3  0,28). Коэффициент
0,28). Коэффициент  для сталей не зависит от знака нагрузки, т.е. одинаков и при растяжении и при сжатии.
для сталей не зависит от знака нагрузки, т.е. одинаков и при растяжении и при сжатии.
 (7)
(7)


