Продольные и поперечные деформации
Под действием продольной силы стержень изменяет свою длину (деформируется – удлиняется или укорачивается). Приращение длины стержня Δℓ; – абсолютная линейная деформация его. Рассмотрим участок стержня элементарной длины dz (рисунок 11 а). Видим, что после приложения нагрузки – продольной силы
Рисунок 11. Продольная (а) и поперечная (б) деформация элементарного участка стержня
Знаем, что относительная продольная деформация определяется отношением
На достаточном удалении от мест приложения внешней силы (гипотеза Сен-Венана) сечения после нагружения остаются плоскими, и перемещаются параллельно самим себе (гипотеза Бернулли – плоских сечений). Следовательно, по всему сечению действуют нормальные напряжения одинаковой величины: σ=const. Отсюда следует постоянство продольной деформации по высоте и ширине сечения ε = const. Тогда, суммируя абсолютные удлинения малых элементов Δdz = εdz по всей длине стержня, получим:
Относительная продольная деформация стержня при простом растяжении:
Легко видеть, что и в направлении осей X и Y поперечное сечение стержня также деформируется – поперечные размеры сечения уменьшаются при его растяжении и увеличиваются при сжатии (рисунок 4 б). Это есть поперечная деформация: абсолютная (Δa и Δb) и относительная:
Они записаны со знаком минус, т.к. продольная и поперечная деформации имеют обратные знаки. Отметим, что для изотропных материалов
|
, где A – площадь поперечного сечения стержня, данный участок получит абсолютную линейную деформацию Δdz.
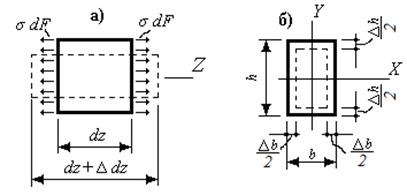
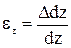. (1)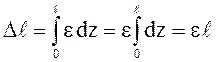
. [м, см, мм] (2)
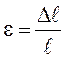. [%] (3)
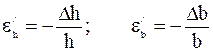. (4)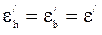
.
