ПРИМЕР 6. Пусть поток поступлений непрерывен, доходы ежегодно увеличиваются на 10%, начальный доход равен 25Пусть поток поступлений непрерывен, доходы ежегодно увеличиваются на 10%, начальный доход равен 25. Капитальные вложения равны 100. Исходные данные: K = 100; R 0 = 25; n OK = Пусть теперь поступления дохода не изменяются во времени. Тогда по формуле (6.10) находим n OK = Далеко не всякий уровень дохода при всех прочих равных условиях приводит к окупаемости инвестиций, если применять дисконтный метод. Срок окупаемости существует, если не нарушаются определенные соотношения между доходами и размером инвестиций. Так: · если постоянные доходы поступают ежегодно, то R > iK; · при поступлении доходов в виде p -срочной ренты R > p [(1 + i)1/ p - 1] K; · при непрерывном поступлении доходов R > ln(1 + i) K или R > · если доход поступает непрерывно и изменяется с некоторым постоянным темпом роста Приведенные неравенства, вероятно, окажутся полезными для быстрой оценки сложившейся ситуации. Если указанные требования не выполняются, то инвестиции не окупятся за любой срок. Он в этом случае будет равен бесконечности. В то же время срок окупаемости, подсчитанный без учета фактора времени, при нарушении указанных условий обязательно будет иметь некоторое конечное значение, что искажает действительное положение дел.
Рис. 6.4
|
= ln 1,1; 
= 0,15.
= 4,5 года.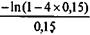
= 6,1 года.
K;
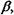то 
.
