Математическое приложение. а. Некоторые стандартные функции
а. Некоторые стандартные функции ln е x = х; (е x)' = е x ; (аx)' = ax ln а;
б. Производная и интеграл функции у = е at. Для расчета современной стоимости и наращенной суммы непрерывного потока платежей необходимо определить производную и интеграл функции у = е at, где а — постоянная величина, t — продолжительность потока платежей.
Соответственно при наращении и дисконтировании по непрерывной ставке
В свою очередь, первообразная для функции е at имеет вид e at / a, так как в силу (1) (е at / а) ' = е at. Отсюда
При использовании непрерывной ставки
в. Определение интеграла
Воспользуемся формулой (2), после чего
Если речь идет о непрерывном дисконтировании по ставке
г. Определение современной стоимости "треугольного" потока платежей На основе рис. 5.2 получим
Общий принцип определения современной стоимости потока платежей:
Применим соотношение (4), после чего
После небольших преобразований получим
Воспользовавшись (2) и (3), окончательно имеем:
д. Доказательство формулы (5. 14) Исходные условия: R 0 = 0; М = Теперь на основе (5) получим
|

 = е n - 1;
= е n - 1;
 . (1)
. (1) имеем:
имеем: .
. . (2)
. (2) получим следующие коэффициенты приведения и наращения постоянного потока платежей:
получим следующие коэффициенты приведения и наращения постоянного потока платежей: .
. . Интегрируем функцию F по частям.
. Интегрируем функцию F по частям. .
.
 , то а = -
, то а = - 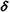 и, следовательно,
и, следовательно, . (3)
. (3) (4)
(4)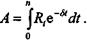
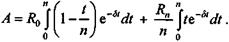

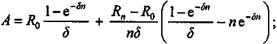
 (5)
(5) ; Rn =
; Rn = 




