ПРИМЕР 6. Пусть по каким-либо причинам момент начала отдачи в примере 1 (вариант А) отодвигается, например, всего на один год

Пусть по каким-либо причинам момент начала отдачи в примере 1 (вариант А) отодвигается, например, всего на один год. В этом случае

N _A = -214,9 + 377,1 х 1,1^-1 = 127,9.

Теперь этот вариант заметно проигрывает по величине чистого приведенного дохода по сравнению с вариантом Б.

Что касается продолжительности периода отдачи, то его чрезмерное увеличение создает иллюзию повышения эффективности. Однако размеры отдаленных во времени доходов вряд ли можно считать вполне надежными и обоснованными. Кроме того, затраты и поступления, ожидаемые в далеком будущем, мало влияют на величину чистого приведенного дохода и ими, как правило, можно пренебречь. Проиллюстрируем сказанное. Пусть речь идет о доходе, поступающем в виде постоянной ренты. Зависимость N от срока ренты п показана на рис. 5.3. В начальный момент N = -K. В точке п = а капиталовложения точно окупаются поступившими доходами. По мере увеличения срока поступлений дохода увеличивается величина N. Однако прирост ее замедляется, а само значение N стремится к некоторому пределу A.

Рис. 5.3

 

Выбор момента, относительно которого дисконтируются члены потока платежей (focal date),также влияет на величину N. Обычно для этого выбирается начало реализации проекта. Сдвиг вперед момента времени для оценивания N увеличивает абсолютные значения обеих составляющих чистого приведенного дохода.

Пусть в проекте предусматриваются мгновенные капиталовложения K и постоянная отдача в течение n лет в виде постоянной ренты постнумерандо, отдача ожидается спустя t лет после начала реализации проекта. При приведении потока платежей к начальному моменту получим:

N = Ra_{n ; l} v^t - K.

В свою очередь, оценивая проект на начало периода отдачи, имеем:

N = Ra_n;i - K (1 + i)^t.

Последнее выражение можно получить, умножая предыдущее равенство на множитель наращения (1 + i) ^t. В общем виде имеем:

N_t = N ₀ (1 + i) ^t,

Рис. 5.4

где N ₀; N_t — величины чистого приведенного дохода, рассчитанные на начало реализации инвестиционного процесса и некоторый момент со сдвигом, равным t.

При сравнении нескольких проектов должно соблюдаться естественное требование — этот момент должен быть общим для всех проектов. Заметим также, что предпочтительный вариант проекта остается таковым при любом выборе момента. Знак величины N не изменяется при сдвиге момента для оценивания.

Проследим теперь влияние процентной ставки на величину N. Из (5.7) следует, что с ростом ставки приведения размер чистого приведенного дохода сокращается. Зависимость N от ставки i для случая, когда вложения осуществляются в начале инвестиционного процесса, а отдачи примерно равномерные, видна на рис. 5.4.

Как показано на рис. 5.4, когда ставка приведения достигает величины J, финансовый эффект от инвестиций оказывается нулевым. Ставка J является важной характеристикой в инвестиционном анализе. Ее содержание и метод расчета обсуждаются в гл. 6. Здесь же отметим, что любая ставка, меньшая, чем J, приводит к положительной оценке N (точки а и b),и, наоборот, дисконтирование по ставке выше J дает отрицательную величину чистого приведенного дохода (точка с)при всех прочих равных условиях. Изменение ставки приведения оказывает заметное влияние на абсолютную величину N. Например, для

Рис. 5.5

условий, согласно которым инвестиции осуществляются равномерно в течение 3 лет ежегодно по 100, а доходы будут поступать 7 лет также по 100 денежных единиц, находим следующие значения N в зависимости от уровня процентной ставки:

i
N	220,8	105,0	28,8	-22,2

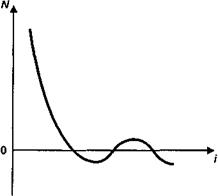
Нулевая величина чистого приведенного дохода в этом примере имеет место при условии i = J = 17,5%.

Для наблюдаемых в практике потоков платежей зависимость не будет столь гладкой и "правильной", как на рис. 5.3. Картина рассматриваемой зависимости становится иной, если члены потока меняют знаки больше одного раза. Например, в силу того что через определенное количество лет после начала отдачи предусматривается модернизация производства, требующая значительных затрат. В этом случае кривая зависимости N от i будет заметно отличаться от кривой на рис. 5.4. Так, на рис. 5.5 показана ситуация, когда величина N трижды меняет свой знак.

Влияние размеров затрат и доходов на N очевидно. Величина N находится в линейной зависимости от каждого из указанных показателей. Причем, чем отдаленнее срок поступления или затрат, тем меньше это влияние.

Теперь остановимся на сравнении (ранжировании) нескольких вариантов проекта по величине N. На первый взгляд, представляется, что такое сравнение весьма условно, так как N зависит от уровня ставки. Однако итог ранжирования проектов обладает высокой устойчивостью (инвариантностью) по отношению к ставке приведения. Для пояснения обратимся к случаю, когда сравниваются три проекта. Обозначим их как А, Б и В. Капиталовложения во всех случаях мгновенные, а потоки доходов представляют собой постоянные ренты постнумерандо с одинаковыми сроками, но разными размерами отдачи. Потоки платежей и расчетные значения N и J показаны в табл. 5.3. Наибольшие значения N и J уварианта Б. При расчете N применена ставка 12%.

Таблица 5.3

t	А	Б	В
	-20	-25	-25
...	...	...	...
N	8,25	14,55	8,90
J (%)	21,4	25,0	20,2

Кривые зависимости N от i для вариантов А и Б показаны на рис. 5.6. Как видим, для любых значений i положительные значения N варианта Б больше, чем у А. В свою очередь, при сравнении вариантов А и В (см. рис. 5.7) обнаруживаем, что чистый приведенный доход по варианту В больше, чем у А при применении любой ставки, вплоть до 15,1%. Если ставка приведения превышает этот уровень, то места проектов по уровню чистого приведенного дохода меняются.

Приведенный пример иллюстрирует тот факт, что выбор процентной ставки часто совсем не сказывается на ранжировании проектов или не оказывает на него влияние в большом диапазоне значений ставки. Точка пересечения кривых А и В

Рис. 5.6 Рис. 5.7

является критической, или барьерной (см. гл. 3). Барьерная точка определяется из равенства чистых приведенных доходов ("конкурирующие" функции) двух сравниваемых проектов: N _A = N _b. Из данного равенства следует

,

где v — дисконтный множитель по неизвестной барьерной ставке j;

R _{A t} и R _{B t} — чистые доходы от проектов по варианту А и В.

Барьерная ставка определяется так же, как и внутренняя норма доходности (см. § 6.1).