Соотношения относительных измерителей эффективности
Относительные финансовые показатели эффективности инвестиций имеют сходную задачу и базируются в конечном счете на одной методике — сопоставлении доходов и затрат. Однако каждый из них решает задачу под своим углом зрения. Можно ожидать, что подобные измерители взаимосвязаны, причем в общем динамика одного показателя непропорциональна изменению другого. Знакомство с такими зависимостями полезно для лучшего понимания существа рассмотренных показателей и их применения в практических ситуациях. Зависимости между попарно взятыми показателями эффективности легко выявить аналитическим путем для случаев, когда поток доходов может быть представлен в виде дискретной финансовой ренты, а капиталовложения мгновенны. Для того чтобы обнаружить интересующие нас связи в общем виде, этого достаточно. Ниже приведены две группы соотношений: между дисконтированными показателями эффективности, между дисконтированными и бухгалтерскими измерителями. Доказательство каждого из этих соотношений базируется на принципе финансовой эквивалентности (см. § 6.9). Начнем с двух важнейших показателей первой группы — чистого приведенного дохода и внутренней нормы доходности.
Рис. 6.6
На основе формул (5.1) и (5.2) находим следующую зависимость: N = R (an;i - аn;J). (6.18) Здесь i — ставка, которая применяется при определении чистого приведенного дохода N. Величина N оказывается положительной, если i < J. Графическая иллюстрация данной зависимости представлена на рис. 6.6. Зависимость внутренней нормы доходности и дисконтированного срока окупаемости определяется следующим образом (см. § 6.9):
С повышением срока окупаемости внутренняя норма доходности сокращается. График этой зависимости представлен на рис. 6.7. Зависимость внутренней нормы доходности и индекса доходности получим на основе формул (5.2) и (5.4):
Рис. 6.7
Графическая иллюстрация данного соотношения показана на рис. 6.8. Как следует из формулы (6.20), при J = 0 имеем U = 0, при J = i имеем U = 1; наконец, если J > i, то U > 1.
Рис. 6.8
Последняя зависимость этой группы — индекс доходности и срок окупаемости. На основе (5.3) и (5.4) имеем
График зависимости представлен на рис. 6.9.
Рис. 6.9
Остановимся теперь на некоторых соотношениях показателей второй группы. Найдем соотношения рентабельности с индексом доходности, дисконтированным сроком окупаемости и внутренней нормой доходности.
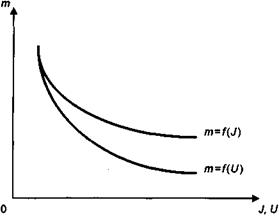
Две первые зависимости иллюстрируются на рис. 6.10. Рентабельность прямо пропорциональна индексу доходности. Коэффициент пропорциональности больше единицы и зависит от размера ставки i. Напомним, что при i = 0 an;i = n. Рассмотрим соотношения срока окупаемости и дисконтированных показателей эффективности (зависимость т и п OKбыла показана выше, см. (6.12)). Получим:
Срок окупаемости обратно пропорционален индексу доходности и равен коэффициенту приведения ренты, рассчитанному по внутренней норме доходности. Графики соответствующих зависимостей см. на рис. 6.11.
Рис. 6.10
Приведенные соотношения получены для частного случая, когда капиталовложения мгновенны, а отдача от них представляет собой ограниченную постоянную ренту постнумерандо. В действительности поток доходов далеко не всегда следует указанной закономерности, отклоняясь от нее в ту или иную сторону. В силу этого найденные строгие зависимости "размываются".
Рис. 6.11
|


 . (6.19)
. (6.19)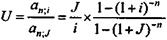 . (6.20)
. (6.20)

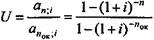 . (6.21)
. (6.21)
 ;
;  ;
;  .
.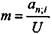 ; т = an;J.
; т = an;J.