Корені многочлена. Теорема Вієта

Дата добавления: 2014-10-22; просмотров: 4303

Теорема (про раціональні корені многочлена). Якщо раціональне число ( , – цілі взаємно прості числа) – корінь многочлена з цілими коефіцієнтами, то – дільник вільного члена, – дільник старшого коефіцієнта.

Висновок 1. Раціональні корені зведеного многочлена – цілі.

Висновок 2. Цілі корені – дільники вільного члена.

Теорема Вієта. Якщо - корені многочлена , то

При одержимо многочлен , і для його коренів справедливо, що

Для зведеного многочлена будемо мати

Приклад 1.5. Знайти корені многочлена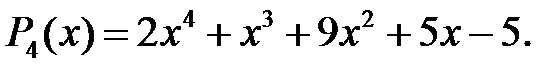

Розв’язання.Знайдемоспочатку раціональні корені. Оскільки то раціональними коренями можуть бути тільки числа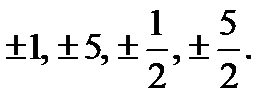

Одержані числа перевіряємо на можливість бути коренями многочлена: отже, не є корінь, а – корінь многочлена.

Розділимо многочлен на (кажуть: виділимо корінь ):

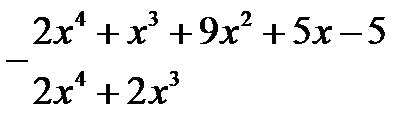
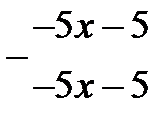
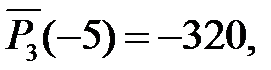
Задачу зведено до знаходження коренів многочлена Якщо крайні коефіцієнти одержаного многочлена прості, то складають нову послідовність чисел, які можуть бути коренями. Одне і те ж число може бути коренем декілька раз, тому перевіримо: отже, є коренем тільки один раз. Продовжимо перевірку інших чисел: Виділимо знайдений корінь

Одержаний многочлен коренів не має. Корені цього многочлена:

Приклад 1.6. Знайти корені многочлена

Розв’язання. Оскільки многочлен зведений, то його раціональні корені – цілі. Цілі корені – дільники вільного члена, а саме: Маємо:

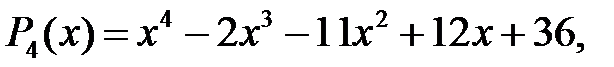
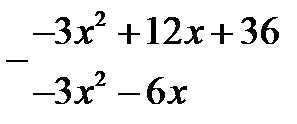
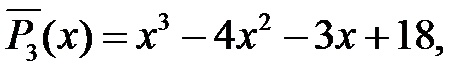претендентів на корені стало менше:

Вилучені раніше числа перевіряти не треба, а потрібно перевірити ще раз:

Отже,

Після знаходження кратного кореня одержимо рівняння Розв’язуючи його, знаходимо

Завдання для самостійної роботи

1.11. Розв’язати квадратні рівняння за теоремою Вієта:

1) 2) 3) 4)

5) 6) 7) 8)

1.12. Знайти дійсні корені многочленів:

1) 2)

3) 4)

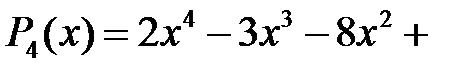
1.13. Розв’язати рівняння в області дійсних чисел:

1) 2)

3) 4)