
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Графіки показникової та логарифмічної функцій
Дата добавления: 2014-10-22; просмотров: 1190
|
|
Означення.Функція вигляду  де
де 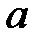 – будь-яке додатне число, що не дорівнює
– будь-яке додатне число, що не дорівнює  , а
, а  – будь-яке дійсне число, називаєтьсяпоказниковою. Графіки показникової функції для значень
– будь-яке дійсне число, називаєтьсяпоказниковою. Графіки показникової функції для значень  і
і  наведено на рис. 4.17.
наведено на рис. 4.17.
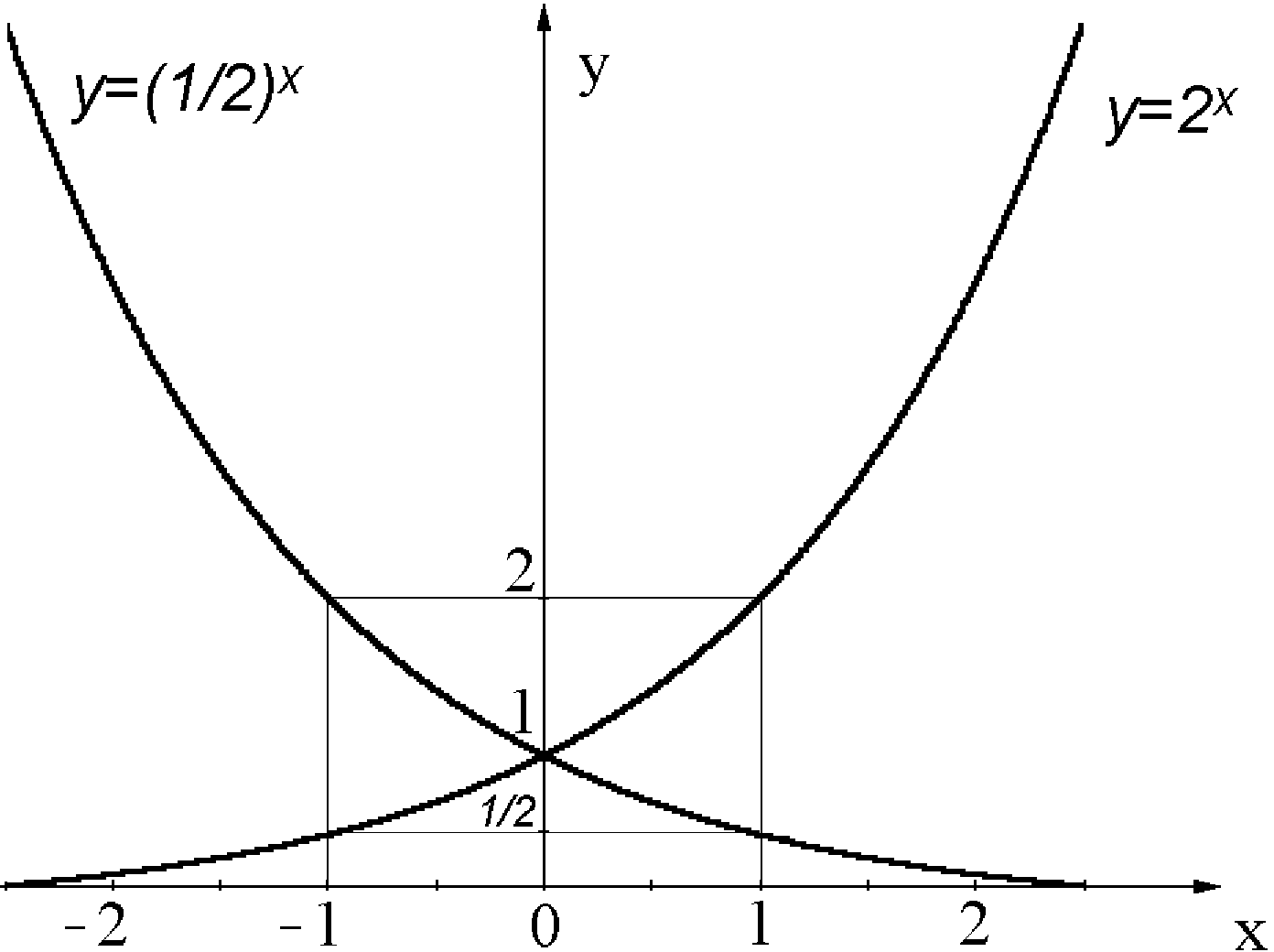

Рис. 4.17 Рис. 4.18
Означення.Функція вигляду  де
де  і
і  , називається логарифмічною. Графіки логарифмічної функції для значень
, називається логарифмічною. Графіки логарифмічної функції для значень  і
і  наведено на рис. 4.18.
наведено на рис. 4.18.
4.5. Графіки обернених тригонометричних функцій
Оберненими тригонометричними функціями називаються функції  ,
,  ,
,  ,
,  .
.
1.  . Область визначення функції:
. Область визначення функції:  область змінювання функції –
область змінювання функції –  Ця функція – обернена до функції
Ця функція – обернена до функції  . Графік функції наведено на рис. 4.19. Основні тототожності:
. Графік функції наведено на рис. 4.19. Основні тототожності:



 Рис. 4.19
Рис. 4.19
|  Рис. 4.20
Рис. 4.20
|
2.  . Область визначення функції:
. Область визначення функції: 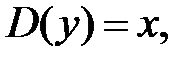
 область змінювання функції –
область змінювання функції –  ,
,  . Ця функція – обернена до функції
. Ця функція – обернена до функції  . Графік функції наведено на рис. 4.20. Основні тототожності:
. Графік функції наведено на рис. 4.20. Основні тототожності:


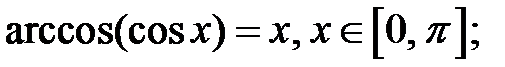

3. 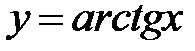 . Область визначення функції:
. Область визначення функції:  , область змінювання функції –
, область змінювання функції –  ,
, 
 – горизонтальні асимптоти при
– горизонтальні асимптоти при 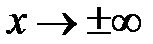 . Ця функція – обернена до функції
. Ця функція – обернена до функції  ,
,  . Графік функції наведено на рис. 4.21. Основні тототожності:
. Графік функції наведено на рис. 4.21. Основні тототожності:



4.  . Область визначення функції:
. Область визначення функції:  , область змінювання функції –
, область змінювання функції –  ,
,  ;
;  і
і  – горизонтальні асимптоти при
– горизонтальні асимптоти при 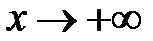 і
і  відповідно. Ця функція – обернена до функції
відповідно. Ця функція – обернена до функції  . Графік функції наведено на рис. 4.22. Основні тототожності:
. Графік функції наведено на рис. 4.22. Основні тототожності:



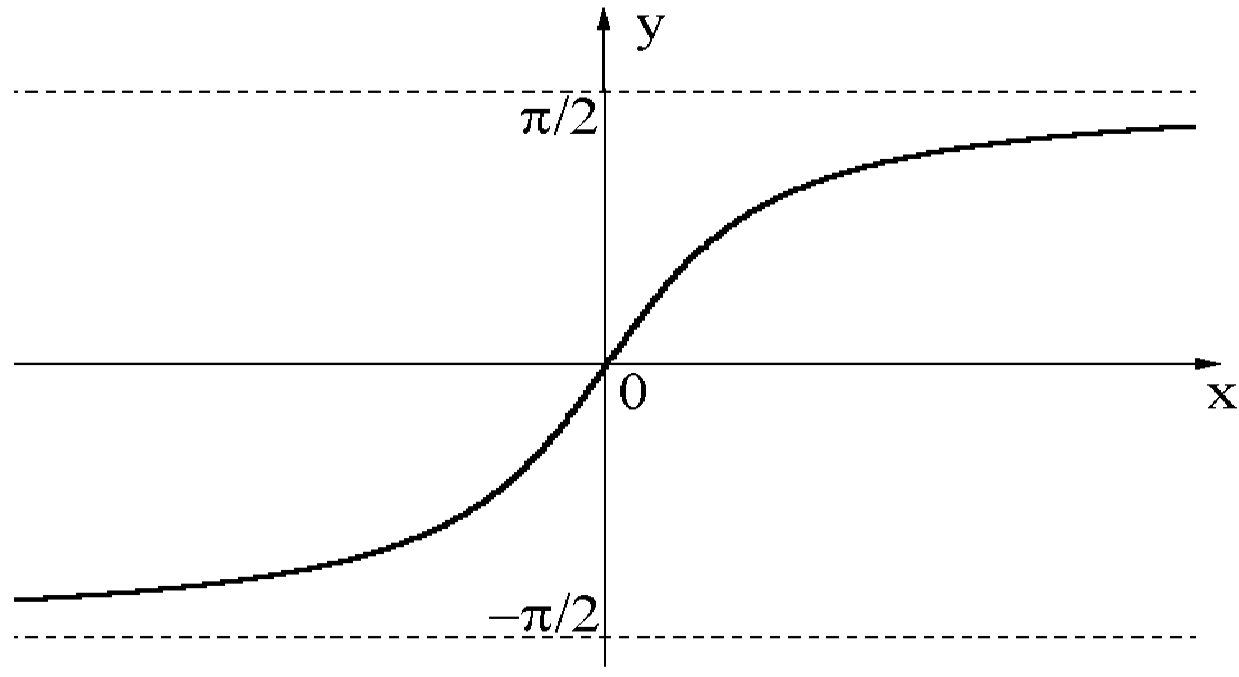

Рис. 4.21 Рис. 4.22
Приклад 4.8. Побудувати графік функції 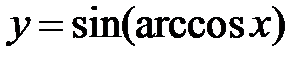 .
.
Розв’язання. Оскільки  , то
, то

Таким чином, 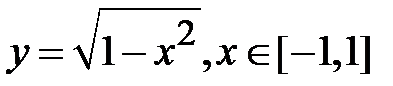 . Графіком цієї функції є напівколо одиничного радіуса, розташоване у верхній півплощині (рис. 4.23).
. Графіком цієї функції є напівколо одиничного радіуса, розташоване у верхній півплощині (рис. 4.23).

Рис. 4.23
| <== предыдущая лекция | | | следующая лекция ==> |
| Графіки алгебраїчних функцій | | | Побудова графіків функцій за допомогою геометричних перетворень |