
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Рівняння та нерівності, що містять під знаком абсолютної величини
Дата добавления: 2014-10-22; просмотров: 1193
|
|
Нагадаємо означення модуля або абсолютної величини числа: модулем  називається само число
називається само число  , якщо
, якщо  і
і  , якщо
, якщо  :
:
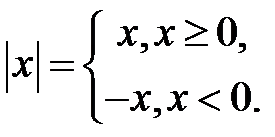
Наприклад, якщо 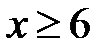 , то
, то  . А у випадку
. А у випадку  значення модуля таке:
значення модуля таке:  .
.
Геометричний зміст модуля:  - це відстань від точки
- це відстань від точки 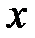 до точки 0 на числовій прямій. Отже, для
до точки 0 на числовій прямій. Отже, для  маємо:
маємо:
а)  (рис. 5.5); б)
(рис. 5.5); б) 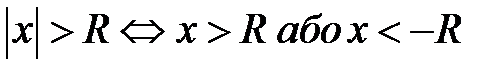 (рис. 5.6);
(рис. 5.6);
в) 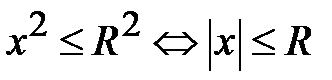 .
.

Рис. 5. 5 Рис. 5. 6 Рис. 5. 7
Корисно запам’ятати також, що 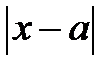 є відстанню на числовій прямій від точки
є відстанню на числовій прямій від точки 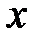 до точки
до точки  (рис. 5.7).
(рис. 5.7).
Наприклад , на числовій прямій множина точок, що задовольняє умову 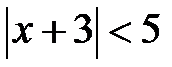 , є інтервал із центром у точці
, є інтервал із центром у точці  і радіусом
і радіусом  , тобто інтервал від точки
, тобто інтервал від точки  до точки
до точки 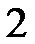 .
.
Приклад 5.12. Розв’язати рівняння  .
.
Розв’язання. Точка  розбиває числову вісь на два проміжки, а саме, якщо
розбиває числову вісь на два проміжки, а саме, якщо 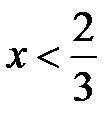 , то вираз під знаком модуля додатний, тому модуль збігається із самим виразом, і маємо систему
, то вираз під знаком модуля додатний, тому модуль збігається із самим виразом, і маємо систему  або
або 
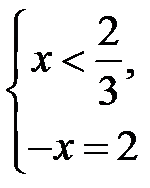 та її розв’язок
та її розв’язок 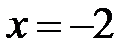 . У протилежному випадку після розкриття знака модуля
. У протилежному випадку після розкриття знака модуля 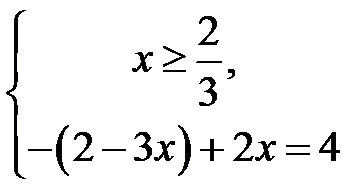 отримаємо
отримаємо 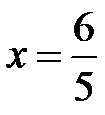 . Відповідь:
. Відповідь:  .
.
Приклад 5.13. Розв’язати рівняння  .
.
Розв’язання. Для розв’язання цього рівняння краще безпосередньо проаналізувати означення модуля. Модуль числа дорівнює 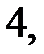 якщо це число
якщо це число  або
або  . Наше рівняння можна замінити на два окремих рівняння, які часто записують у вигляді сукупності
. Наше рівняння можна замінити на два окремих рівняння, які часто записують у вигляді сукупності  Кожне рівняння розглянемо окремо і отримаємо
Кожне рівняння розглянемо окремо і отримаємо 
Приклад 5.14. Розв’язати рівняння 
Розв’язання. Перший спосіб - використання заміни змінної, а саме: позначимо 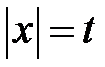 і підкреслимо, що
і підкреслимо, що  . Розв’язками отриманого квадратного рівняння
. Розв’язками отриманого квадратного рівняння  є числа
є числа 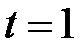 і
і 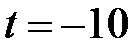 , друге із яких нас не влаштовує. Рівняння
, друге із яких нас не влаштовує. Рівняння 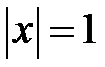 має два корені:
має два корені: 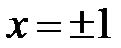 .
.
Рівняння можна було розв’язати інакше, а саме розглянути окремо два випадки: 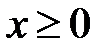 і
і  . Відповідно маємо
. Відповідно маємо 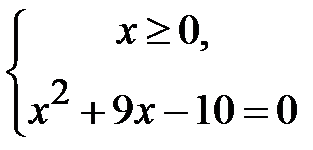 і
і 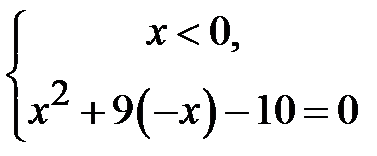 . Першу систему задовольняє число
. Першу систему задовольняє число  , а другу –
, а другу –  .
.
Приклад 5.15. Розв’язати нерівність  .
.
Розв’язання. Нерівність одразу замінимо на  або
або  . Відповідь:
. Відповідь:  або
або 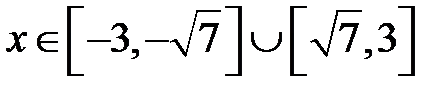 .
.
Приклад 5. 16. Розв’язати нерівність 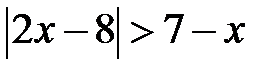 .
.
Розв’язання. Щоб позбавитися знака модуля, розглянемо окремо два випадки: 1)  , 2)
, 2) 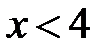 , які приводять до двох окремих систем:
, які приводять до двох окремих систем:
1)  і 2)
і 2)  . Перша має розв’язок
. Перша має розв’язок  , а друга - розв’язок
, а друга - розв’язок 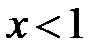 . Тому
. Тому 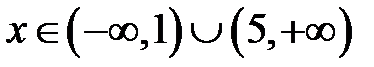 .
.
Зауваження. Розглянуті приклади здаються занадто простими, але у подальшому вони можуть змінювати своє “обличчя” та виникати у досить серйозному вигляді, а тоді має неабияке значення вміння розв’язувати їх швидко та правильно
( див. завдання 5.10)
Завдання для самостійної роботи
5.7. Розв’язати рівняння:
а)  ; b)
; b)  ; c)
; c)  ; d)
; d) 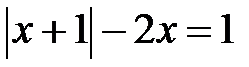 .
.
5.8. Розв’язати рівняння  .
.
5.9. Зобразити на числовій осі точки, що задовольняють нерівності:
а)  ; b)
; b)  ; c)
; c)  ; d)
; d) 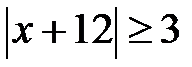 ; e)
; e) 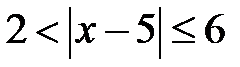 ; f)
; f)  ;
;
g)  .
.
5.10. Визначити, для яких значень  геометрична прогресія із знаменником
геометрична прогресія із знаменником  буде нескінченно спадною, тобто
буде нескінченно спадною, тобто 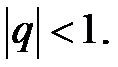
5.11. Розв’язати нерівності: а) 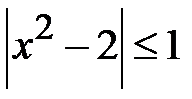 ; b)
; b)  .
.
5.12. Розв’язати рівняння:
а) 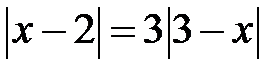 ; b)
; b)  ; c)
; c) 
5.13. Розв’язати нерівності:
а)  ; b)
; b) 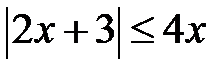 ; c)2
; c)2  ; d)
; d) 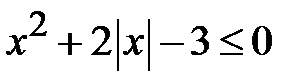 .
.
5.4. Показникові та логарифмічні рівняння
Рівняння, що містять невідому в показникові степеня, мають назву “показникові рівняння”.
Основні види показникових рівнянь такі:
1. 
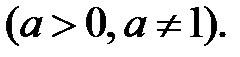
За визначенням нульового показника 
2. 

Якщо розділити обидві частини рівняння на 
 то одержимо рівняння
то одержимо рівняння 
3. 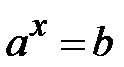
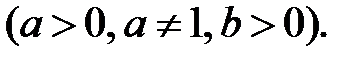
За означенням логарифма 
4. 
Винесемо за дужки  де
де  Маємо
Маємо
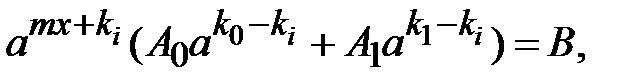 або
або 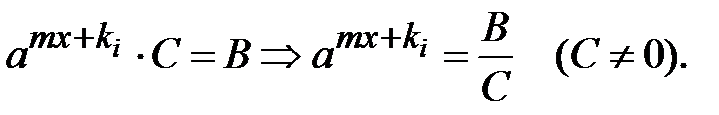
Рівняння має розв`язок , якщо  .
.
5. 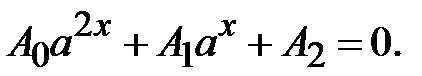
Позначимо  , тоді одержимо квадратне рівняння відносно
, тоді одержимо квадратне рівняння відносно 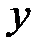 , оскільки
, оскільки 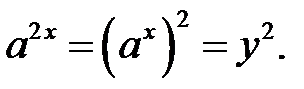
6. 
Поділивши обидві частини на 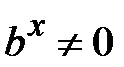 , отримаємо рівняння, що має вигляд рівняння 5 .
, отримаємо рівняння, що має вигляд рівняння 5 .
Приклад5.17. Розв’язати рівняння 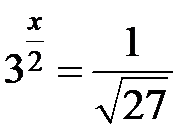 .
.
Розв’язання. Праву частину  перетворимо в число з основою 3:
перетворимо в число з основою 3:  . Тепер підставимо
. Тепер підставимо 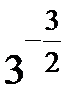 в рівняння. Маємо
в рівняння. Маємо  Þ
Þ  .
.
Приклад5.18.Розв’язати рівняння 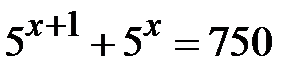 .
.
Розв’язання. Оскільки  , то рівняння матиме вигляд
, то рівняння матиме вигляд 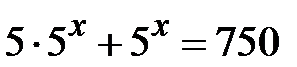 . Винесемо
. Винесемо  за дужки:
за дужки: 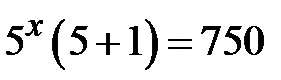 Þ
Þ  Þ
Þ  Таким чином,
Таким чином, 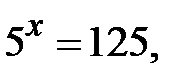 але
але  Þ
Þ  Þ
Þ  .
.
Приклад5.19. Розв’язати рівняння 
Розв’язання. Позначимо  , тоді
, тоді 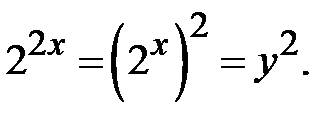 Підставимо
Підставимо  і
і 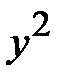 в задане рівняння. Отримаємо квадратне рівняння
в задане рівняння. Отримаємо квадратне рівняння 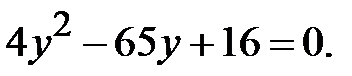 Розв’яжемо це рівняння. Маємо:
Розв’яжемо це рівняння. Маємо: Þ
Þ 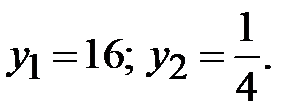 Звідси:
Звідси:  ,
,  ,
, 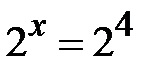 ,
,  і
і  ,
,  ,
,  ,
, 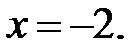
Приклад 5.20. Розв’язати рівняння 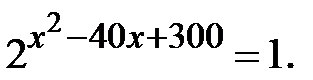
Розв’язання. 
Приклад 5.21. Розв’язати рівняння 
Розв’язання. 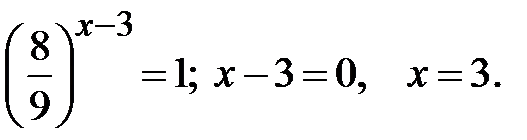
Приклад 5.22 . Розв’язати рівняння 
Розв’язання. Винесемо за дужки  Отримаємо:
Отримаємо:

Приклад 5.23. Розв’язати рівняння 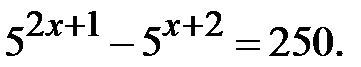
Розв’язання. Позначимо  . Маємо
. Маємо  . Корені квадратного
. Корені квадратного
рівняння:  і
і  . Оскільки
. Оскільки  то нас влаштовує тільки корінь
то нас влаштовує тільки корінь  . Тоді
. Тоді 
Якщо невідома змінна міститься під знаком логарифма або в його основі, то таке рівняння називається логарифмічним. При розв’язуванні логарифмічних рівнянь обов’язково потрібно враховувати властивості логарифмічної функції  :
:  ,
,  ,
,  .
.
Приклад 5.24. Розв’язати рівняння 
Розв’язання. Для цього рівняння ОДЗ таке: 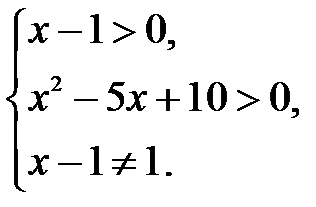
Розв’яжемо нерівність  :
:  Парабола
Парабола 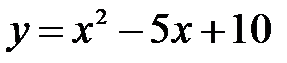 не має точок перетину з віссю
не має точок перетину з віссю 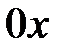 . Отже,
. Отже,  для будь-яких
для будь-яких  . Тоді
. Тоді 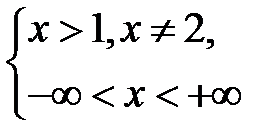 Þ
Þ 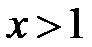 ,
,  . За означенням логарифма
. За означенням логарифма 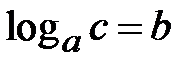 маємо
маємо
 Þ
Þ 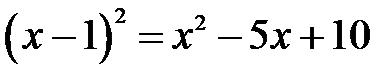 Þ
Þ 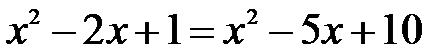 Þ
Þ  ,
,  .
.
Приклад 5.25 . Розв’язати рівняння  .
.
Розв’язання. Визначимо ОДЗ цього рівняння:  Þ
Þ  .
.
До лівої частини рівняння застосуємо властивість 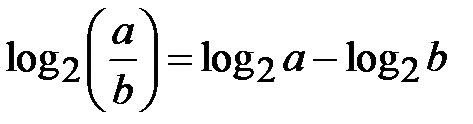 , тобто ліва частина дорівнює логарифму дробу
, тобто ліва частина дорівнює логарифму дробу  В правій частині рівняння
В правій частині рівняння  . Тоді початкове рівняння набуде вигляду
. Тоді початкове рівняння набуде вигляду  За означенням логарифма
За означенням логарифма 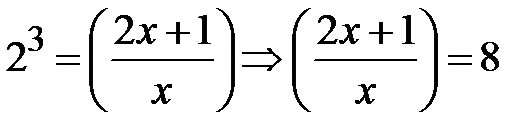 . Оскільки
. Оскільки 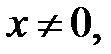 то
то 
 .
.
Приклад 5.26. Розв’язати рівняння 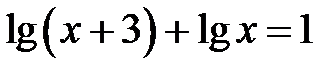 .
.
Розв’язання. Для цього рівняння ОДЗ таке: 
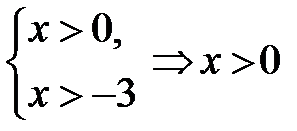 . До лівої частини рівняння застосуємо властивість
. До лівої частини рівняння застосуємо властивість 
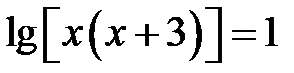 . За означенням десяткового логарифма
. За означенням десяткового логарифма  ,
,  ,
,  ,
,  . Врахуємо, що
. Врахуємо, що 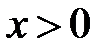 , тоді
, тоді 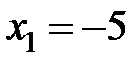 не є коренем цього рівняння.
не є коренем цього рівняння.
Завдання для самостійної роботи
5.14. Розв’язати рівняння:
а) 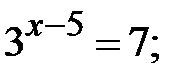 b)
b)  c)
c) 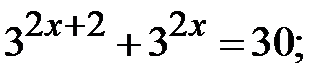 d)
d) 
e) 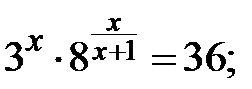 f)
f)  g)
g) 
h) 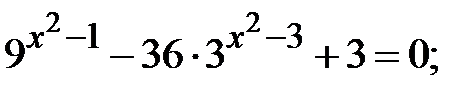 i)
i) 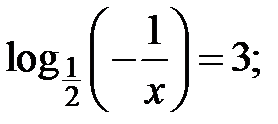 j)
j) 
k)  l)
l) 
m) 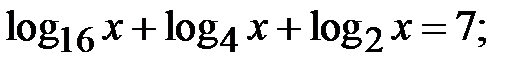 n)
n)  o)
o) 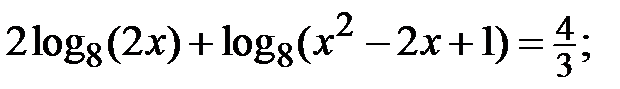 p)
p) 
5.5. Показникові та логарифмічні нерівності
При розв’язуванні нерівностей, що містять показникову або логарифмічну функцію, треба пам’ятати властивості цих функцій, а саме те, що 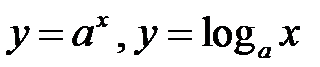 при
при  є монотонно зростаючими, а при
є монотонно зростаючими, а при  – монотонно спадними. Таким чином, маємо нерівності
– монотонно спадними. Таким чином, маємо нерівності
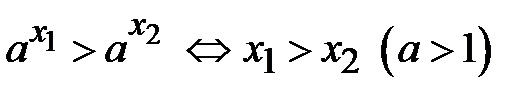 ;
;  .
.
Аналогічно:
 .
.
При розв’язуванні логарифмічних нерівностей також треба пам’ятати, що функція  визначена тільки при
визначена тільки при  .
.
Приклад 5.27 . Розв язати нерівність 
Розв’язання. Оскільки функція  – монотонно зростаюча і
– монотонно зростаюча і 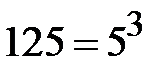 , то нерівність, задана за умовою, еквівалентна таким нерівностям:
, то нерівність, задана за умовою, еквівалентна таким нерівностям:
 ,
, 
(застосовано метод інтервалів для розв’язування нерівностей).
Приклад 5.28. Розв’язати нерівність 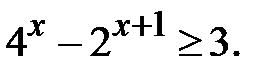
Розв’язання. Покладемо  . Тоді
. Тоді  . Враховуючи, що
. Враховуючи, що
 , одержимо
, одержимо 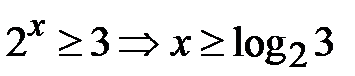 .
.
Приклад 5.29 . Розв’язати нерівність 
Розв’язання. ОДЗ цієї нерівності така: 
Оскільки  – монотонно спадна функція, то задана нерівність еквівалентна нерівності
– монотонно спадна функція, то задана нерівність еквівалентна нерівності 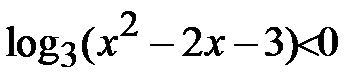 . Остання нерівність з урахуванням того, що
. Остання нерівність з урахуванням того, що  – монотонно зростаюча функція, рівносильна нерівності
– монотонно зростаюча функція, рівносильна нерівності 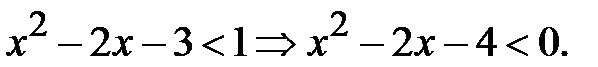 З урахуванням ОДЗ одержимо відповідь:
З урахуванням ОДЗ одержимо відповідь:  (рис. 5.8).
(рис. 5.8).

Рис. 5.8
Приклад 5.30. Розв’язати нерівність 
Розв’язання. Зведемо праву частину до основи  :
:  , одержимо
, одержимо  . Функція
. Функція  - монотонно спадна. Тому, якщо
- монотонно спадна. Тому, якщо  , а
, а  і
і 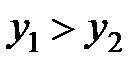 , то
, то  . Отже, з нерівності
. Отже, з нерівності  випливає
випливає  , або
, або 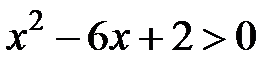 . Розв’яжемо квадратну нерівність:
. Розв’яжемо квадратну нерівність:
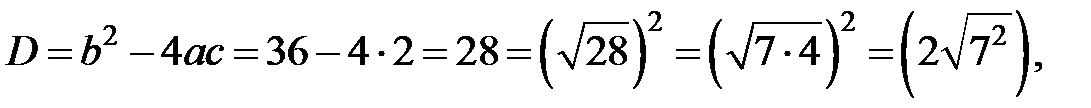
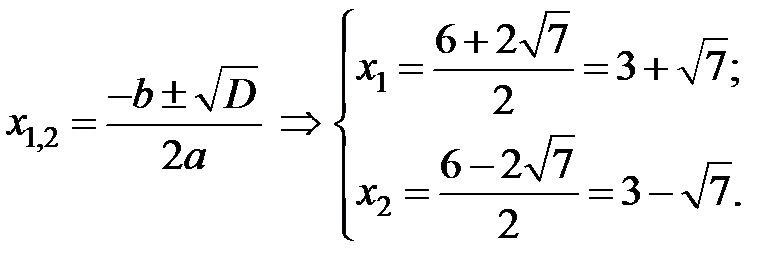
Таким чином, 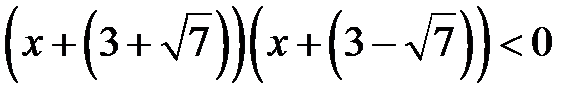 Þ
Þ  (рис. 5.9).
(рис. 5.9).
Приклад 5.31. Розв’язати нерівність 
Розв’язання. Врахуємо, що  Тоді
Тоді  а функція
а функція 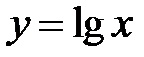 монотонно зростає. Це означає, що для будь-яких
монотонно зростає. Це означає, що для будь-яких  і
і 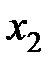 (при
(при  ), що належать області допустимих значень функції,
), що належать області допустимих значень функції,  . Тоді, якщо
. Тоді, якщо  то
то 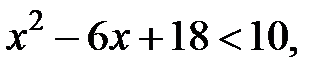
 Розв’яжемо квадратну нерівність:
Розв’яжемо квадратну нерівність: 
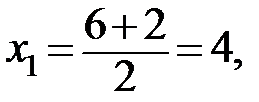
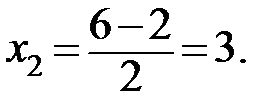 Тоді
Тоді
 Þ
Þ 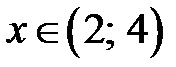 (рис. 5.10).
(рис. 5.10).


Рис. 5.9 Рис. 5.10
Завдання для самостійної роботи
5.16. Розв’язати нерівності:
а) 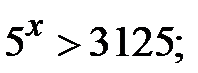 b)
b)  c)
c)  d)
d)  e)
e) 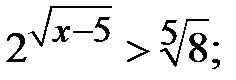
f) 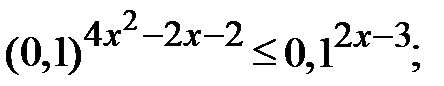 g)
g)  h)
h) 
i)  j)
j)  k)
k) 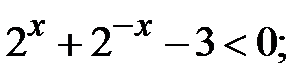 l)
l)  m)
m)  n)
n) 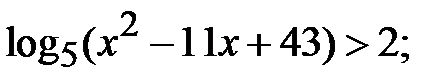
o)  p)
p) 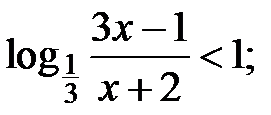 q)
q) 
| <== предыдущая лекция | | | следующая лекция ==> |
| Розв’язання. | | | Тригонометричні рівняння |