Означення комплексного числа

Дата добавления: 2014-10-22; просмотров: 894

У шкільному курсі математики розглядаються такі числові множини: натуральні числа , цілі числа , раціональні числа і дійсні числа . При цьому , тобто кожна подальша множина включає попередню і більш досконала з погляду можливості виконання операцій. Так, наприклад, на множині натуральних чисел не завжди здійснима операція віднімання (1 - 7 – не визначено в ). На множині цілих чисел ця операція завжди визначена (1 - 7 = - 6).

Проте на множині дійсних чисел не здійснима операція обчислення кореня парного степеня з від’ємного числа ( – не визначено, якщо – парне, а ). Наприклад, рівняння не має розв’язків на множині . Отже, виникає необхідність розширення множини дійсних чисел для одержання всіх можливих коренів алгебраїчних рівнянь.

Рис. 6.1

На множині дійсних чисел рівняння має лише один корінь , але , звідки або , або . Останнє квадратне рівняння має від’ємний дискримінант , тобто не має дійсних розв’язків, його корені мають вигляд . Із застосуванням уявної одиниці одержимо 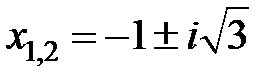. Такий вираз будемо називати алгебраїчною формою запису комплексного числа.

Означення. Комплексним числом у алгебраїчній формі називається вираз вигляду 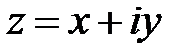, де і – будь-які дійсні числа, а 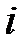– уявна одиниця. Числа і називаються відповідно дійсною і уявною частинами комплексногочисла 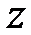і позначаються , .

– множина всіх комплексних чисел. За умови маємо . Отже, – множина дійсних чисел – є підмножиною множини комплексних чисел.

Комплексні числа і вважаються рівними тоді й тільки тоді, коли і .

Комплексне число називається спряженим комплексному числу . Отже, якщо рівняння з дійсними коефіцієнтами має комплексні корені, то вони завжди спряжені.

Комплексне число зображується в комплексній площині точкою з координатами або вектором, початок якого знаходиться в точці , а кінець – в точці , де – це дійсна вісь, а – уявна (рис. 6.1).

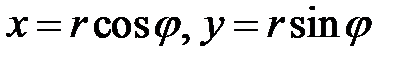Довжина вектора називається модулем комплексного числа і позначається , отже, . Кут , утворений вектором з додатним напрямом осі , називається аргументом комплексного числа і позначається ( або ). Коли , , а якщо , то . З рис. 6.1 видно, що . Тоді . Останній вираз називається тригонометричною формою комплексного числа.