
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Тригонометричні функції числового аргументу
Дата добавления: 2014-10-22; просмотров: 2173
|
|
Наведемо означення тригонометричних функцій числового аргументу.
 Синусом числа
Синусом числа  (
(  ) називається ордината точки C, яка утворюється в результаті повороту радіус-вектора
) називається ордината точки C, яка утворюється в результаті повороту радіус-вектора  = {0,1} на кут
= {0,1} на кут  радіан. Якщо
радіан. Якщо  , то поворот здійснюється проти ходу годинникової стрілки і вважається додатним, а якщо
, то поворот здійснюється проти ходу годинникової стрілки і вважається додатним, а якщо  , то поворот – від’ємний і здійснюється за ходом годинникової стрілки.
, то поворот – від’ємний і здійснюється за ходом годинникової стрілки.
Косинусом числа  (
(  ) називається абсциса точки С.
) називається абсциса точки С.
Тангенсомчисла  (
(  ) називається ордината точки В, яка розташована на перетині продовження радіус-вектора
) називається ордината точки В, яка розташована на перетині продовження радіус-вектора  з віссю тангенсів (пряма, проведена через точку А(1,0) перпендикулярно до осі ОХ).
з віссю тангенсів (пряма, проведена через точку А(1,0) перпендикулярно до осі ОХ).
Котангенсомчисла  (
(  ) називається Рис. 2.1
) називається Рис. 2.1
абсциса точки К, яка лежить на перетині продовження радіус-вектора  з віссю котангенсів (пряма, проведена через точку М(0,1) перпендикулярно до осі ОY).
з віссю котангенсів (пряма, проведена через точку М(0,1) перпендикулярно до осі ОY).
Іноді використовуються ще дві тригогонометричні функції, а саме секанс числа  (
(  ) і косеканс числа
) і косеканс числа  (
(  ). Ці функції вводяться таким чином:
). Ці функції вводяться таким чином:
 ,
,  .
.
Між тригонометричними функціями кута  існують прості співвідношення:
існують прості співвідношення:
 ;
;  ,
,  ;
;
 ,
,  ;
;  ,
,  ;
;
 ,
,  ;
;  ,
,  .
.
 набуває додатних значень у першій (
набуває додатних значень у першій (  ) та другій (
) та другій (  ) чвертях і від’ємних – у третій (
) чвертях і від’ємних – у третій (  ) та четвертій (
) та четвертій (  );
);  набуває додатних значень у першій та четвертій чвертях і від’ємних – у другій та третій;
набуває додатних значень у першій та четвертій чвертях і від’ємних – у другій та третій;  і
і  – додатних у першій та третій чвертях і від’ємних – у другій та четвертій (рис. 2.2).
– додатних у першій та третій чвертях і від’ємних – у другій та четвертій (рис. 2.2).
Згідно з означенням тригонометричних функцій мають місце такі формули:
 ,
,  ,
,  ,
,
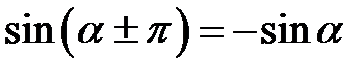 ,
,  ,
, 

Рис. 2.2
для будь-якого значення  і
і
 ,
,  ,
,  ,
, 
для будь-якого допустимого значення  .
.
Табличні значення тригонометричних функцій гострих кутів наведено в табл. 2.1.
Таблиця 2.1
| Функція | Кут  : радіани (градуси) : радіани (градуси)
| ||||

| 
| 
| 
| 
| |
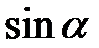
| 
| 
| 
| 
| 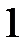
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| – |

| – | 
| 
| 
| 
|
Приклад 2.1. Визначити знаки таких виразів: а)  б)
б) 
в)  де
де  .
.
Розв’язання: а) кут  належить другій чверті, тому
належить другій чверті, тому  ; б) кут
; б) кут  належить першій чверті, тому
належить першій чверті, тому  ; в) значення кута
; в) значення кута  не перевищує
не перевищує  , тому вираз
, тому вираз  належить другій чверті. Синус і косинус кутів другої чверті мають різні знаки, тому
належить другій чверті. Синус і косинус кутів другої чверті мають різні знаки, тому  .
.
Приклад 2.2. Обчислити 
Розв’язання. Аргументи тригонометричних функції – табличні. Значення тригонометричних функцій від цих аргументів – відомі, а саме:



Тому 
Приклад 2.3. Обчислити 
 ,
, 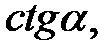 якщо
якщо  і
і  .
.
Розв’язання. Оскільки  , то
, то  або
або  Оскільки
Оскільки  , то
, то 


Завдання для самостійної роботи
2.01.Побудувати кут: 1) синус якого дорівнює: a)  b)
b)  c)
c)  2) косинус якого дорівнює: a)
2) косинус якого дорівнює: a)  b)
b)  c)
c) 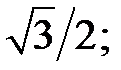 3) тангенс якого дорівнює: a)
3) тангенс якого дорівнює: a)  b)
b)  c)
c)  котангенс якого дорівнює: a)
котангенс якого дорівнює: a)  b)
b)  c)
c)  .
.
2.02. Визначити знаки таких виразів: а)  b)
b)  c)
c) 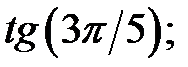
d)  e)
e)  , де
, де  f)
f)  , де
, де 
g)  h)
h) 
2.03.Обчислити: а)  b)
b) 
c)  d)
d) 
e)  f)
f) 
2.04. Для яких чвертей проміжку  виконуються нерівності: а)
виконуються нерівності: а) 
b)  c)
c) 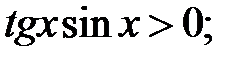 d)
d) 
2.05. До яких чвертей належить кут, якщо: а) 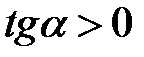 ; b)
; b) 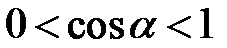 ; c)
; c) 
d) 
2.06. Чи існує таке значення  щоб: а)
щоб: а) 
b)  c)
c) 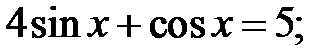 d)
d) 
2.07. Обчислити  ,
,  ,
,  , якщо: а)
, якщо: а)  і
і  b)
b)  і
і 
| <== предыдущая лекция | | | следующая лекция ==> |
| Раціональних дробів на прості дроби | | | Основні формули тригонометрії. Формули зведення. Перетворення тригонометричних виразів |