
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Рівняння та нерівності. Основні означення
Дата добавления: 2014-10-22; просмотров: 1069
|
|
Рівнянням з однією змінною називається рівність, що містить цю змінну, яку називають невідомою.
Розв’язком ( або коренем) рівняння називається таке значення змінної, яке при підстановці його у рівняння перетворює його на правильну числову рівність.
Розв’язати рівняння – це знайти всі його корені або довести, що коренів немає.
Два рівняння  і
і 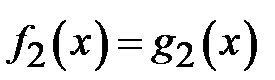 називаються рівносильними, якщо множини їх розв’язків збігаються.
називаються рівносильними, якщо множини їх розв’язків збігаються.
Якщо всі корені рівняння  є коренями рівняння
є коренями рівняння  , то друге рівняння називають наслідком першого.
, то друге рівняння називають наслідком першого.
Для пошуку коренів рівняння над його частинами здійснюють деякі перетворення із метою спрощення, наприклад:
1. Додавання до обох частин одного й того ж виразу.
2. Множення обох частин на один і той же вираз.
3. Скорочення обох частин на один і той же вираз.
4. Піднесення обох частин до одного степеня.
5. Логарифмування або потенціювання обох частин за однаковою основою та ін.
Зауважимо, що при перетвореннях рівняння не завжди зберігається рівносильність,тобто у процесі перетворення можна як втратити корені, так і придбати так звані «зайві».
Проілюструємо сказане на прикладах рівнянь різного вигляду.
Приклад 5.1. Розв’язати ірраціональне рівняння  .
.
Розв’язання. Після визначення ОДЗ рівняння  піднесемо обидві його частини до квадрата і отримаємо
піднесемо обидві його частини до квадрата і отримаємо  або
або  . Корені квадратного рівняння
. Корені квадратного рівняння  . Перевіркою легко переконатись в тому, що число
. Перевіркою легко переконатись в тому, що число  дійсно задовольняє наше рівняння, а от число
дійсно задовольняє наше рівняння, а от число  – ні. Справа в тому, що при піднесенні обох частин до парного степеня неправильна рівність
– ні. Справа в тому, що при піднесенні обох частин до парного степеня неправильна рівність  перетворилась у правильну
перетворилась у правильну 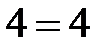 .
.
Приклад 5.2. Розв’язати рівняння 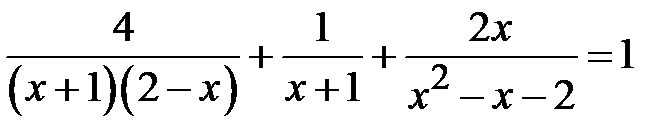 .
.
Розв’язання. ОДЗ:  . Спільний знаменник ліворуч дорівнює добутку
. Спільний знаменник ліворуч дорівнює добутку 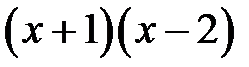 і рівняння перетворюється на
і рівняння перетворюється на  або
або  . Після скорочення маємо
. Після скорочення маємо  , звідки
, звідки  . Але це число не є розв’язком , тому що не задовольняє ОДЗ.
. Але це число не є розв’язком , тому що не задовольняє ОДЗ.
Подальший пошук розв’язків для різноманітних класів рівнянь здійснюється різними методами, серед яких слід особливо зупинитися на методі заміни змінної та методі факторизації (тобто розкладання на множники від слова «factor» – множник).
Метод факторизації можна застосувати для розв’язання кубічних, тригонометричних та інших рівнянь.
Приклад 5.3. Знайти корені рівняння 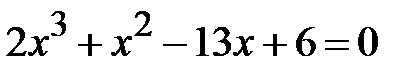 .
.
Розв’язання.Можна спробувати знайти корені спочатку серед чисел  . Число
. Число  перетворює рівняння на тотожність. Тому ліва частина є добутком виразу
перетворює рівняння на тотожність. Тому ліва частина є добутком виразу  і полінома другого степеня, а саме
і полінома другого степеня, а саме  . Рівняння перетворилось на
. Рівняння перетворилось на  , яке має корені
, яке має корені  .
.
Приклад 5.4. Знайти корені рівняння  .
.
Розв’язання. Перепишемо рівняння у вигляді  ,
,
 , що дає дві серії розв’язків
, що дає дві серії розв’язків  і
і  .
.
Зауваження. Не можна скорочувати обидві частини рівняння на спільний множник 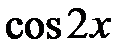 , бо це призводить до втрати першої серії розв’язків.
, бо це призводить до втрати першої серії розв’язків.
Приклад 5.5. Знайти функцію, що є оберненою до функції  .
.
Розв’язання. У нашому прикладі фактично потрібно розв’язати відносно  показникові рівняння
показникові рівняння  . Це є ілюстрацією методу заміни змінної, а саме: позначимо
. Це є ілюстрацією методу заміни змінної, а саме: позначимо 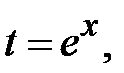
 . Маємо рівняння
. Маємо рівняння  , або
, або  . Його додатний корінь
. Його додатний корінь  , звідки
, звідки  .
.
Дві нерівності  і
і  називаються рівносильними, якщо множини їх розв’язків збігаються. Наприклад:
називаються рівносильними, якщо множини їх розв’язків збігаються. Наприклад:
- Нерівності
 і
і  рівносильні, якщо
рівносильні, якщо 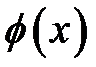 визначена на ОДЗ.
визначена на ОДЗ. - Нерівності
 і
і  рівносильні, якщо
рівносильні, якщо 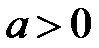 .
. - Нерівності
 і
і  рівносильні, якщо
рівносильні, якщо  .
. - Якщо обидві частини нерівності додатні, то можна підносити їх до степеня.
Приклад 5. 6. Розв’язати нерівність  .
.
Розв’язання. Визначимо ОДЗ:  . Якщо права частина нерівності невід’ємна, тобто виконано умову
. Якщо права частина нерівності невід’ємна, тобто виконано умову 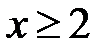 , то маємо право піднести до квадрата
, то маємо право піднести до квадрата 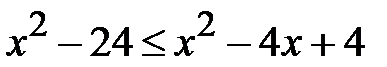 , або
, або  . Узгодження із ОДЗ дає відповідь
. Узгодження із ОДЗ дає відповідь 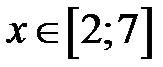 . У випадку, коли права частина від’ємна, ця нерівність не може бути виконана, тому що невід’ємне число (ліворуч) не може бути меншим, ніж від’ємне (праворуч).
. У випадку, коли права частина від’ємна, ця нерівність не може бути виконана, тому що невід’ємне число (ліворуч) не може бути меншим, ніж від’ємне (праворуч).
Приклад 5.7. Розв’язати нерівність 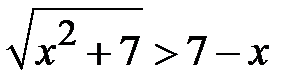 .
.
Розв’язання. На відміну від попереднього прикладу випадок 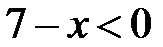 є розв’язком , бо додатне число автоматично буде більшим, ніж від’ємне. Якщо ж
є розв’язком , бо додатне число автоматично буде більшим, ніж від’ємне. Якщо ж  , піднесемо обидві частини до квадрата і отримаємо
, піднесемо обидві частини до квадрата і отримаємо  , або
, або  . Дві частини відповіді
. Дві частини відповіді  і
і  можна об’єднати у множину
можна об’єднати у множину  .
.
Завдання для самостійної роботи
5.1. Переконатись у тому, що рівняння не є рівносильними, і визначити причини:
а)  та
та 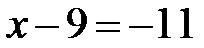 ; b)
; b) 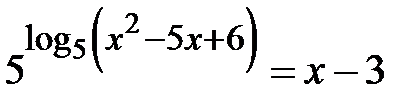 та
та  ; c)
; c)  та
та  ; d)
; d)  та
та  ; e)
; e)  та
та 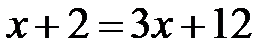 .
.
5. 2. Розв’язати кубічні рівняння:
а)  ; b)
; b)  ; c)
; c)  ;
;
d)  .
.
5. 3. Розв’язати ірраціональні рівняння:
а)  ; b)
; b)  ; c)
; c) 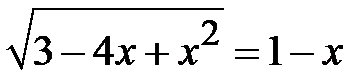 ; d)
; d) 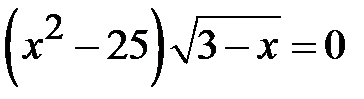 .
.
5. 4. Розв’язати рівняння методом заміни:
а) 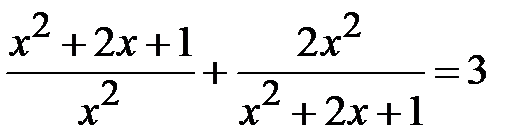 ; b)
; b)  .
.
5. 5. Розв’язати нерівності:
а) 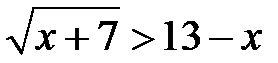 ; b)
; b)  .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Побудова графіків функцій за допомогою геометричних перетворень | | | Метод інтервалів. Раціональні нерівності |