Алгебраїчні дії з комплексними числами

Дата добавления: 2014-10-22; просмотров: 3609

Нехай і . Застосовуючи властивості арифметичних дій, маємо:

1) додавання (віднімання): ;

2) множення:

;

3) ділення:

.

Остання дія була виконана з урахуванням властивості спряжених комплексних чисел: . Завдяки множенню знаменника на його спряжене у знаменнику одержано дійсне число, яке далі розглядається як коефіцієнт.

Піднесення комплексного числа до степеня n та обчислення кореня n-го степеня краще виконувати у тригонометричній формі.

Нехай 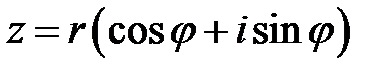. Тоді:

а) піднесення до степеня n: – формула Муавра;

б) обчислення кореня n-го степеня: , .

Зауваження 1. Важливо знати значення різних степенів числа :

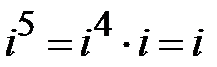, , , , , , … Отже, . Крім того; .

Зауваження 2. З урахуванням властивостей тригонометричних функцій корінь

n-го степеня з будь-якого комплексного числа має рівно n різних значень.

Приклад 6.1. Знайти суму, різницю, добуток і частку комплексних чисел .

Розв’язання: 1) ;

2) ;

3) ;

4) .

Приклад 6.2. Знайти суму, різницю, добуток і частку комплексних чисел .

Розв’язання: 1) ( – дійсне число);

2) ( – уявне число);

3) ( – дійсне число);

4) .

Приклад 6.3.Записати числа 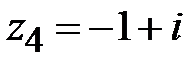, у тригонометричній формі.

Розв’язання.За формулою 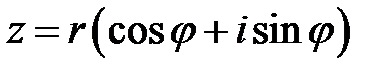, де , а

, знаходимо:

: , , , ;

, , ,

;

: , , , ;

: , , ,

.

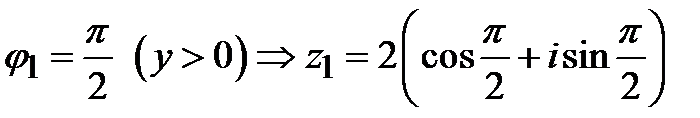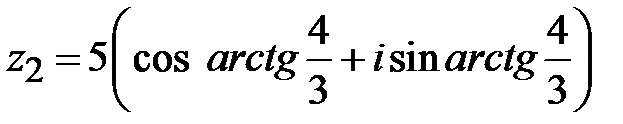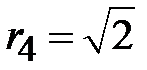Приклад 6.4.Обчислити: а) ; б) .

Розв’язання: а) За формулою 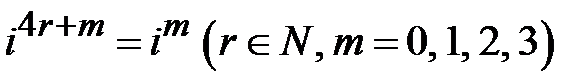маємо

( ).

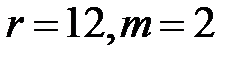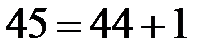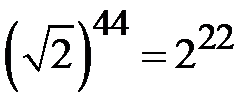б) Якщо , то . Отже, у тригонометричній формі маємо . За формулою Муавра з урахуванням і одержимо

.

Оскільки період функцій і , то аргументи цих функцій краще записати так: . Отже, з урахуванням періодичності відповідних функцій і формул зведення маємо

.

Запишемо останній вираз у алгебраїчній формі. Оскільки , маємо .

Приклад 6.5.Обчислити .

Розв’язання. Оскільки корінь n-го степеня з комплексного числа обчислюється за формулою , запишемо число у тригонометричній формі: , тобто 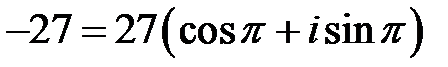. Отже, . Задамо і одержимо три різні корені.

Відповідь: ;

;

(якщо 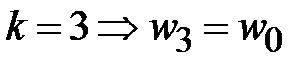, тобто для корені відповідно збігаються).

Зауваження 3. 1) корінь 3-го степеня має три різні значення; 2) арифметичний корінь (на множині дійсних чисел) збігається з ; 3) два інші корені є спряженими комплексними числами: .

Приклад 6.6.Розв’язати рівняння: а) ; б) .

Розв’язання.а) .

б) Такі рівняння легко розв’язувати, якщо виділити повний квадрат. Отже, .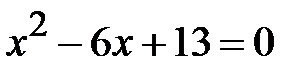

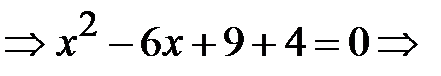
Завдання для самостійної роботи

Обчислити:

6.1. . 6.2. .

6.3. 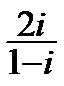. 6.4. . 6.5. . 6.6. .

6.7. . 6.8 . 6.9. . 6.10. .

6.11. . 6.12. . 6.13. . 6.14. .

Розв’язати рівняння та зобразити їхні корені на комплексній площині:

6.15. . 6.16. . 6.17. . 6.18. .

6.19. . 6.20. . 6.21. . 6.22. .