
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Тригонометричні рівняння
Дата добавления: 2014-10-22; просмотров: 1431
|
|
Не існує єдиного методу побудови розв’язку тригонометричних рівнянь. Можна лише зазначити, що перетворення тригонометричних виразів має бути спрямовано на те, щоб рівняння набувало стандартного вигляду або «розпадалося» на кілька стандартних (простіших) рівнянь. Наведемо лише кілька методів побудови розв’язків тригонометричних рівнянь, тим паче що використання їх буде корисним у подальшому вивченні курсу вищої математики:
1. Введення додаткового аргументу за формулою
 .
.
Оскільки  то величини
то величини  і
і  можуть бути косинусом і синусом деякого кута
можуть бути косинусом і синусом деякого кута  . Якщо, наприклад, позначити
. Якщо, наприклад, позначити  , а
, а  , то отримаємо вищенаведену формулу.
, то отримаємо вищенаведену формулу.
2. Зведення рівняння до алгебраїчного після заміни тригонометричної функції.
3. Розкладання на множники.
Слід також запам’ятати розв’язки так званих найпростіших тригонометричних рівнянь:
 ,
,  ,
, 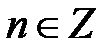 ,
, 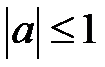 ;
;
 ,
, 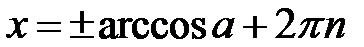 ,
,  ,
,  ;
;
 ,
, 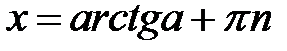 ,
,  ,
,  ;
;
 ,
, 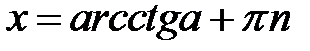 ,
, 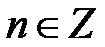 ,
,  .
.
Окрім загальних формул розв’язків найпростіших тригонометричних рівнянь корисно знати формули для так званих «окремих випадків» розв’язків найпростіших тригонометричних рівнянь:
 ,
,  ,
, 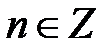 ;
; 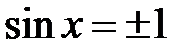 ,
,  ,
,  ;
;
 ,
,  ,
,  ;
;  ,
,  ,
,  ;
;
 ,
,  ,
,  ;
;  ,
,  ,
,  ;
;
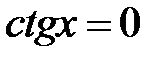 ,
, 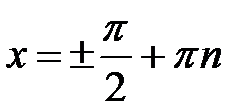 ,
, 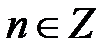 .
.
Приклад 5.32. Розв’язати рівняння 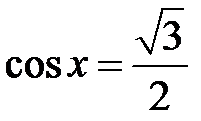 .
.
Розв’язання. Задано рівняння  . Його розв’язок:
. Його розв’язок: 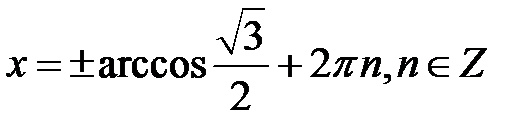 , або
, або  .
.
Приклад 5.33. Розв’язати рівняння  .
.
Розв’язання.Якщо поділити обидві частини на 2, то можна записати рівняння у вигляді  , або
, або  ,
, 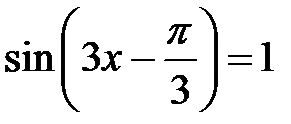 ; звідси
; звідси 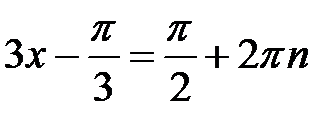 ,
,  ,
,  .
.
Приклад 5.34. Розв’язати рівняння 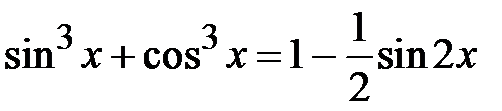 .
.
Розв’язання. Розкладемо ліву частину рівняння на множники, використовуючи формулу суми кубів:


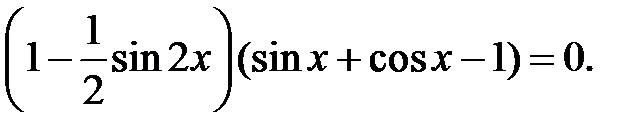
Це рівняння рівносильне сукупності рівнянь

Перше з них розв’язків не має  , а до другого застосуємо такі перетворення:
, а до другого застосуємо такі перетворення:
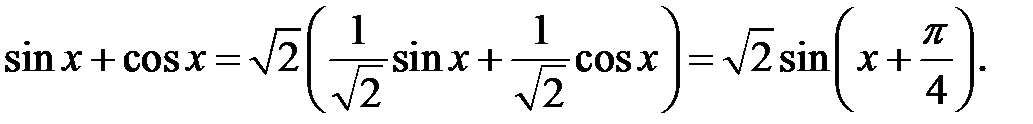
Таким чином,

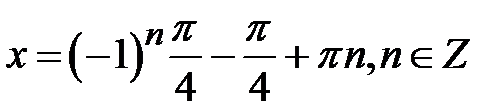 або
або 
Приклад 5.35. Розв’язати рівняння 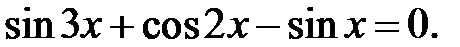
Розв’язання. До лівої частини рівняння застосуємо формулу різниці синусів, а далі отриманий вираз розкладемо на множники. Маємо:


Приклад 5.36. Розв’язати рівняння 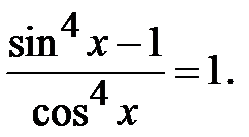
Розв’язання. ОДЗ цього рівняння знаходиться з умови  , тобто
, тобто  . Звільнившись від знаменника,отримаємо
. Звільнившись від знаменника,отримаємо  ,
,  ,
, 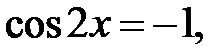
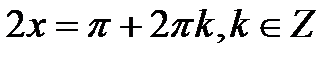 ,
, 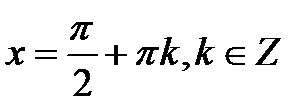 . Остання множина при
. Остання множина при 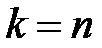 збігається з множиною
збігається з множиною  , яка не входить в ОДЗ. Тому наведене рівняння розв’язків не має.
, яка не входить в ОДЗ. Тому наведене рівняння розв’язків не має.
Приклад 5.37. Розв’язати рівняння 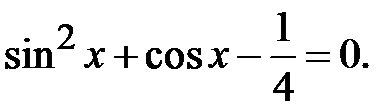
Розв’язання. Скористаємося основною тригонометричною тотожністю і перепишемо рівняння у вигляді
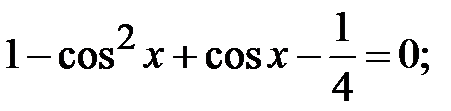

Покладемо  і розв’яжемо квадратне рівняння:
і розв’яжемо квадратне рівняння: 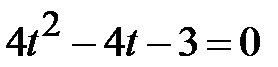 , де
, де 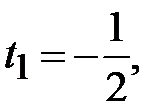
 . Оскільки
. Оскільки  , то рівняння
, то рівняння 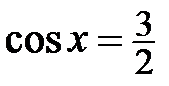 розв’язків не має. Розв’язком рівняння
розв’язків не має. Розв’язком рівняння 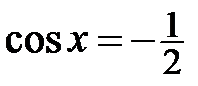 , а значить, і всього рівняння є множина
, а значить, і всього рівняння є множина

Приклад 5.38. Розв’язати рівняння 
Розв’язання. Оскільки для будь-якого розв’язку цього рівняння  , то поділимо це рівняння на
, то поділимо це рівняння на  . Отримаємо рівняння
. Отримаємо рівняння  . Звідси
. Звідси
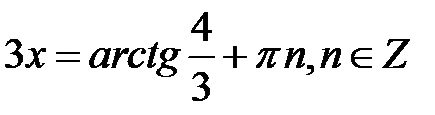 , або
, або  .
.
Приклад 5.39. Розв’язати рівняння 
Розв’язання. Використовуючи формулу подвійного кута, перепишемо рівняння у вигляді  а потім поділимо його на
а потім поділимо його на 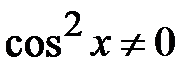 . Отримаємо
. Отримаємо  Останнє рівняння є алгебраїчним рівнянням відносно
Останнє рівняння є алгебраїчним рівнянням відносно  , а саме
, а саме 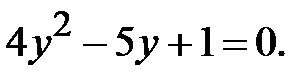 Розв’язок цього рівняння такий:
Розв’язок цього рівняння такий: 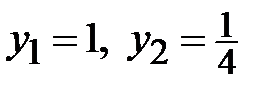 . Маємо:
. Маємо:
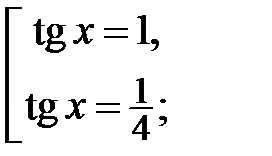
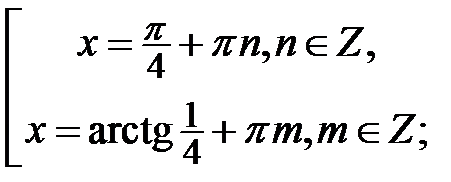
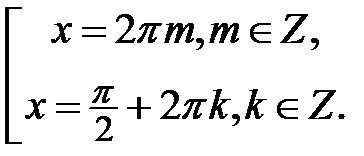
Завдання для самостійної роботи
5.18. Розв’язати найпростіші тригонометричні рівняння:
а)  ; b)
; b) 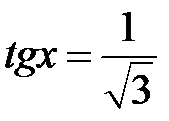 ; c)
; c) 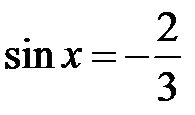 ; d)
; d) 
e) 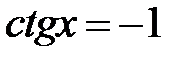 ; f)
; f) 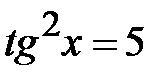 ; g)
; g) 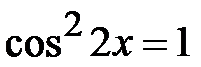 ; h)
; h) 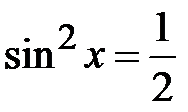 .
.
Розв’язки рівнянь зобразити на тригонометричному колі.
Розв’язати тригонометричні рівняння:
5.19. а) 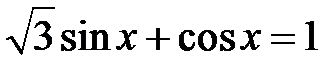 ; b)
; b)  ; c)
; c) 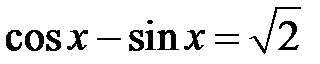 ;
;
d) 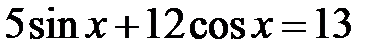 ; e)
; e) 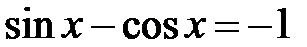 ; f)
; f) 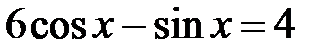 .
.
5.20. 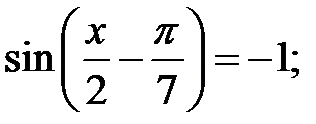 5.21.
5.21.  5.22.
5.22. 
5.23.  5.24.
5.24.  5.25.
5.25. 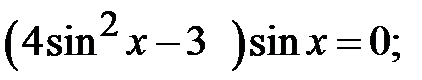
5.26. 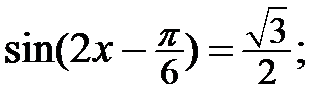 5.27.
5.27. 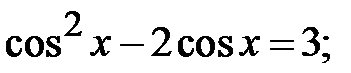 5.28.
5.28. 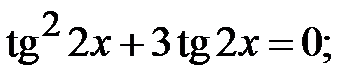
5.29. 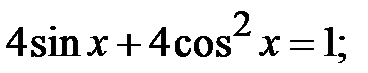 5.30.
5.30. 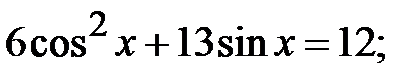 5.31.
5.31. 
5.32. 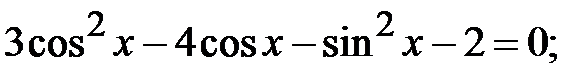 5.33.
5.33. 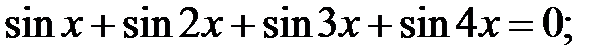
5.34.  5.35.
5.35. 
5.36. 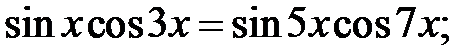 5.37.
5.37. 
5.38. 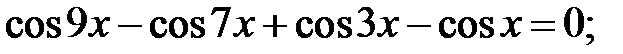 5.39.
5.39. 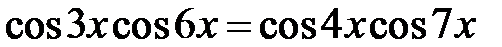 .
.
5.7 Тригонометричні нерівності
Розв’язання тригонометричних нерівностей зводиться, як правило, до розв’язання найпростіших тригонометричних нерівностей вигляду 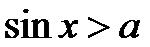 ,
, 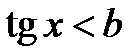 і
і
т. п., а також до розв’язання сукупностей або систем тригонометричних нерівностей. Для розв’язання найпростіших тригонометричних нерівностей зручно користуватися тригонометричним колом. Множина значень змінної величини, яка задовольняє дану найпростішу нерівність, зображується на тригонометричному колі у вигляді однієї або кількох дуг. При цьому зазначимо, що якщо точка кола відповідає числу  , то вона відповідає і всім числам вигляду
, то вона відповідає і всім числам вигляду 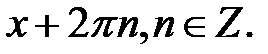
Приклад 5.40. Розв’язати нерівність 
Розв’язання. За означенням  – це абсциса точки на тригонометричному колі (рис. 5.11), яка відповідає числу
– це абсциса точки на тригонометричному колі (рис. 5.11), яка відповідає числу 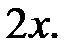 Відкладемо на колі точки, які мають абсциси, що дорівнюють (
Відкладемо на колі точки, які мають абсциси, що дорівнюють ( 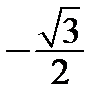 ). Це точки А
). Це точки А 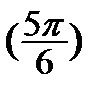 і B
і B  . Геометричним розв’язком наведеної нерівності буде замкнена дуга AmB тому, що
. Геометричним розв’язком наведеної нерівності буде замкнена дуга AmB тому, що
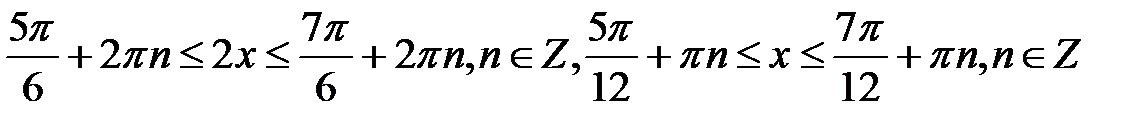 , або
, або

 Рис. 5.11
Рис. 5.11
| 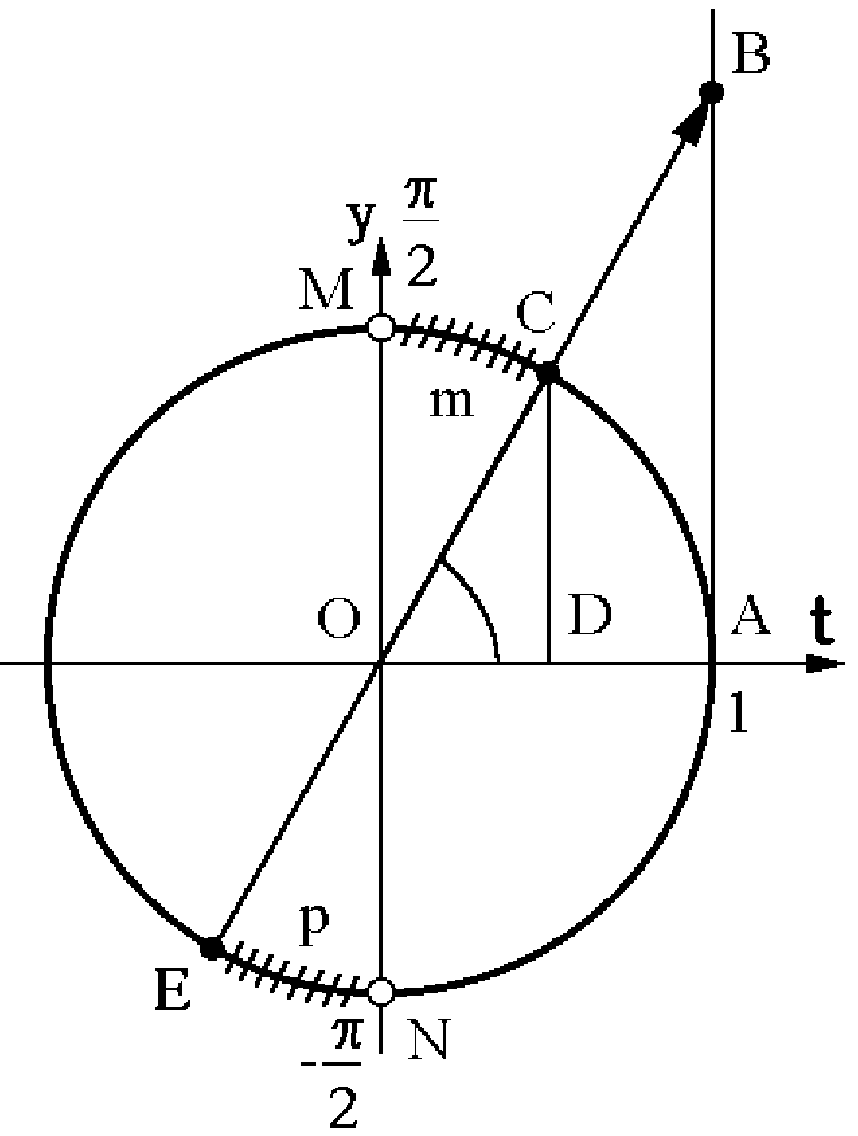 Рис. 5.12
Рис. 5.12
|
Приклад 5.41. Розв’язати нерівність  .
.
Розв’язання. Функція 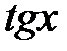 не визначена в точках
не визначена в точках  і
і  при
при 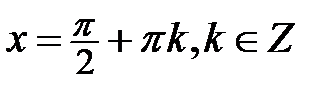 (рис. 5.12). Проведемо вісь тангенсів
(рис. 5.12). Проведемо вісь тангенсів 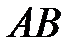 перпендикулярно до осі абсцис
перпендикулярно до осі абсцис 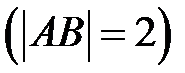 . Промінь
. Промінь  перетинає одиничне коло в точці С
перетинає одиничне коло в точці С  :
:
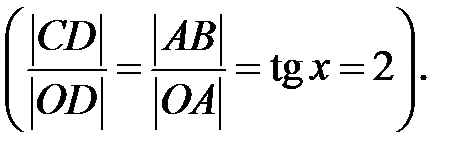
Функція 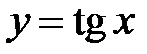 монотонно зростає при
монотонно зростає при  тому нерівність
тому нерівність  буде виконуватися для всіх точок відкритої дуги СmМ. Оскільки головний період функції
буде виконуватися для всіх точок відкритої дуги СmМ. Оскільки головний період функції 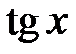 дорівнює
дорівнює  , то наведена нерівність буде виконуватися для всіх точок дуги ЕрN. Складемо аналітичний запис вказаних дуг:
, то наведена нерівність буде виконуватися для всіх точок дуги ЕрN. Складемо аналітичний запис вказаних дуг:
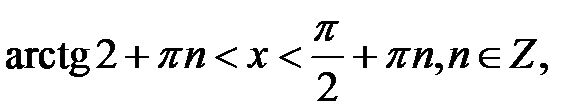

Приклад 5.42. Розв’язати нерівність  .
.
Розв’язання. Перепишемо нерівність у вигляді


Остання нерівність рівносильна системам нерівностей
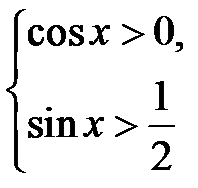 (1) і
(1) і  (2)
(2)
Геометричний розв’язок систем (1) і (2) подано на рис. 5.13 і 5.14 відповідно. Це будуть дуги AmC і FpM. Об’єднуючи ці дуги, запишемо аналітичний запис розв’язків:
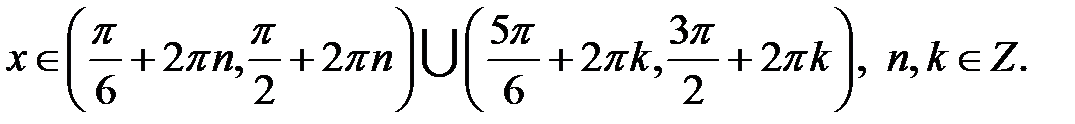
Приклад 5.43. Розв’язати нерівність 
Розв’язання. Запропоновану тригонометричну нерівність перетворимо до алгебраїчної нерівності відносно величини  :
:



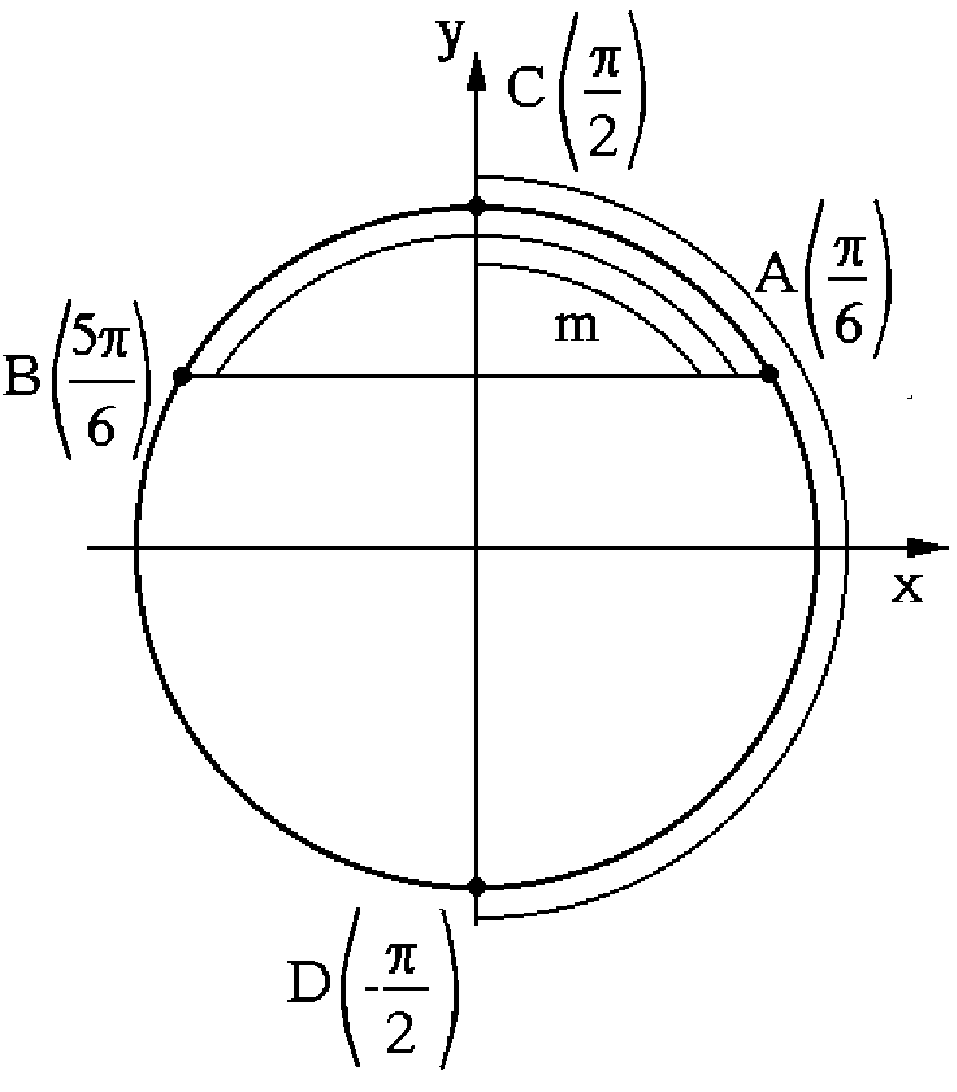 Рис. 5.13
Рис. 5.13
|  Рис. 5.14
Рис. 5.14
|
Розв’язком останньої нерівності є сукупність множин:
 або
або 
Геометричний розв’язок тригонометричних нерівностей зображено на рис. 5.15 і 5.16. Це дуги DmC, EpF, SpR і PmQ.
 Рис. 5.15
Рис. 5.15
|  Рис. 5.16
Рис. 5.16
|
Аналітичним розв’язком наведеної нерівності буде множина

Завдання для самостійної роботи
Розв’язати тригонометричні нерівності:
5.40.  5.41.
5.41.  5.42.
5.42.  5.43.
5.43. 
5.44.  5.45.
5.45.  5.46.
5.46. 
5.47.  5.48.
5.48.  5.49
5.49 
| <== предыдущая лекция | | | следующая лекция ==> |
| Рівняння та нерівності, що містять під знаком абсолютної величини | | | Означення комплексного числа |