
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Розв’язання.
Дата добавления: 2014-10-22; просмотров: 917
|
|
1. Нулі заданої функції –  . Вони розбивають числовий інтервал на 4 проміжки (рис. 5.3). Оскільки нерівність не строга, то точки
. Вони розбивають числовий інтервал на 4 проміжки (рис. 5.3). Оскільки нерівність не строга, то точки  і
і  включаємо до розв’язку.
включаємо до розв’язку.

Рис. 5.3
2. Визначаємо знак нерівності на інтервалі  : візьмемо
: візьмемо  , тоді
, тоді  .
.
3. Подвійних точок нерівність не має. Тому скористаємося умовою зміни знака:  – "+";
– "+";  – "-";
– "-";  – "+". Маємо
– "+". Маємо  .
.
Приклад 5.11.Розв’язати нерівність 
Розв’язання. ОДЗ:  . Відмітимо на числовій прямій точки
. Відмітимо на числовій прямій точки  ,
,  (нулі чисельника) і
(нулі чисельника) і  ,
,  (нулі знаменника). Нерівність записано в стандартному вигляді, тому праворуч від точки
(нулі знаменника). Нерівність записано в стандартному вигляді, тому праворуч від точки  функція додатна. Усі показники степеня непарні, тому при переході через них знак лівої частини нерівності буде змінюватися (рис. 5.4). Маємо
функція додатна. Усі показники степеня непарні, тому при переході через них знак лівої частини нерівності буде змінюватися (рис. 5.4). Маємо 

Рис. 5. 4
Завдання для самостійної роботи
5.6. Розв’язати нерівності:
а)  ; b)
; b)  ; c)
; c) 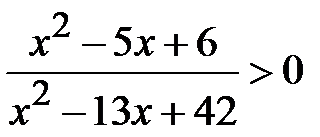 ;
;
d)  ; e)
; e)  ; f)
; f) 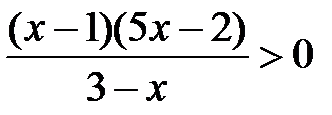 ;
;
g)  ; h)
; h) 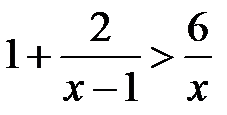 ;
;
i)  ; j)
; j) 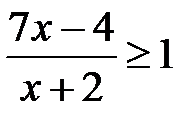 ; k)
; k)  ; l)
; l)  .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Метод інтервалів. Раціональні нерівності | | | Рівняння та нерівності, що містять під знаком абсолютної величини |