
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Українське художнє килимарство і ткацтво.
Дата добавления: 2015-08-31; просмотров: 812
|
|
| Обозначения: V — объем; Sполн — площадь полной поверхности; Sбок — площадь боковой поверхности; Sо — площадь основания; Pо — периметр основания; Pо — периметр перпендикулярного сечения; l — длина ребра; h — высота. Формула Эйлера N − L + F = 2 N — число вершин, L — число ребер, F — число граней выпуклого многогранника. | |

| |
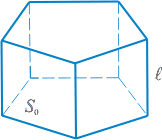
Призма — многранник, две грани которого — равные многоугольники, расположенные в параллельных плоскостях, а остальные — параллелограммы.

| 
|
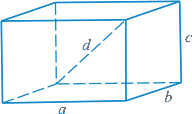
Параллелепипед — призма, основание которой — параллелограмм. Параллелепипед имеет шесть граней и все они — параллелограммы.
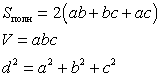
| 
|
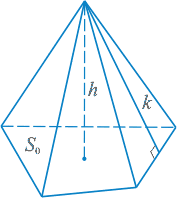
Пирамида — многранник, у которого одна грань n-угольник — основание пирамиды, а остальные боковые грани — треугольники с общей вершиной — вершиной пирамиды.
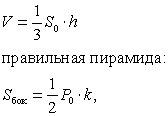 где k — апофема где k — апофема
| 
|

| |
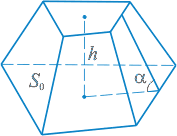
Если в пирамиде провести сечение параллельное основанию, то тело, ограниченное этим сечением, основанием, и заключенной между ними боковой поверхностью пирамиды, называетсяусеченной пирамидой.
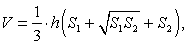 где S1 и S2 — площади оснований где S1 и S2 — площади оснований
 где α — двугранный угол при ребре нижнего основания. где α — двугранный угол при ребре нижнего основания.
| 
|

| |
| Правильные многогранники Многогранник называется правильным, если все его грани — равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны. Существует пять различных правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр). Обозначения: а — длина ребра; V — объем; Sбок — площадь боковой поверхности; Sполн — площадь полной поверхности; R — радиус описанной сферы; r — радиус вписанной сферы; h — высота. | |

| |
Тетраэдр — четыре грани — равносторонние равные треугольники. Тетраэдр имеет четыре вершины и шесть ребер

| 
|

| |
Куб — шесть граней — равные квадраты. Куб имеет восемь вершин и двенадцать ребер.
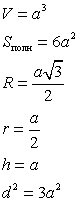
| 
|

| |
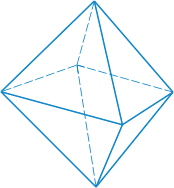
Октаэдр — восемь граней — равносторонние равные треугольники. Октаэдр имеет шесть вершин и двенадцать ребер
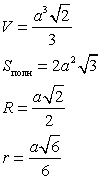
| 
|

| |
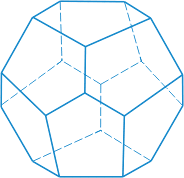
Додекаэдр — двенадцать граней — правильные равные пятиугольники. Додекаэдр имеет двадцать вершин и тридцать ребер.
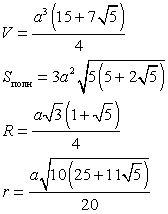
| 
|

| |
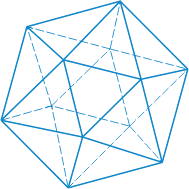
Икосаэдр — двадцать граней — равносторонние равные треугольники. Икосаэдр имеет двенадцать вершин и тридцать ребер.
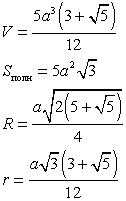
| 
|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
| <== предыдущая лекция | | | следующая лекция ==> |
| Російське художнє скло 18-19 ст. | | | Білет №19 |