
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Білет №19
Дата добавления: 2015-08-31; просмотров: 1273
|
|
« Многогранники»
Завдання І-го рівня
1. Обчислити об’єм піраміди, основою якої є прямокутник зі сторонами 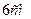 і
і
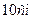 , а висота піраміди дорівнює
, а висота піраміди дорівнює 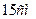 .
.
2. Сторона основи правильної трикутної призми дорівнює 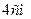 , а її бічне
, а її бічне
ребро - 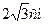 . Обчислити об’єм призми.
. Обчислити об’єм призми.
3. Обчислити площу бічної поверхні прямої призми, основою якої є
паралелограм зі сторонами 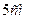 і
і 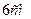 , а бічне ребро дорівнює
, а бічне ребро дорівнює 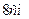 .
.
4. Обчислити площу бічної поверхні правильної шестикутної піраміди, сторона
основи якої дорівнює 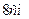 , а апофема -
, а апофема - 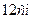 .
.
5. Ребро куба збільшили у 2 рази. У скільки разів збільшився об’єм куба?
6. Обчислити об’єм піраміди, основою якої є паралелограм зі сторонами 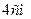 і
і
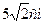 та кутом
та кутом 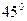 між ними, а висота піраміди дорівнює
між ними, а висота піраміди дорівнює 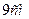 .
.
7. Обчислити площу бічної поверхні прямої призми, основа якої трикутник зі сторонами
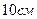 ,
, 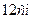 ,
, 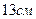 , а бічне ребро дорівнює
, а бічне ребро дорівнює 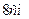 .
.
8. Обчислити об’єм правильної трикутної призми, сторона основи якої дорівнює 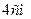 , а
, а
бічне ребро - 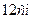 .
.
Завдання ІІ-го рівня
9. Основа прямої призми – ромб з діагоналями 10см і 24см . Менша діагональ призми
дорівнює 26см . Обчисліть площу бічної поверхні призми.
10. Сторони основи прямого паралелепіпеда дорівнюють 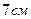 і
і 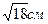 , кут між ними
, кут між ними 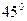 .
.
Менша діагональ утворює кут 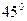 з площиною основи. Знайдіть об’єм паралелепіпеда.
з площиною основи. Знайдіть об’єм паралелепіпеда.
11. Сторона основи правильної трикутної піраміди дорівнює 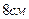 , а бічна грань нахилена до
, а бічна грань нахилена до
площини основи під кутом 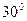 . Знайдіть площу повної поверхні піраміди.
. Знайдіть площу повної поверхні піраміди.
12. Бічна грань правильної чотирикутної піраміди нахилена до площини основи під кутом 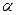 .
.
Відрізок, який сполучає середину висоти піраміди і середину апофеми, дорівнює 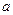 .
.
Знайдіть об’єм піраміди.
13. Сторони перпендикулярного перерізу, який перетинає всі ребра нахиленого паралелепіпеда,
дорівнюють 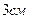 і
і 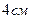 та складають між собою кут
та складають між собою кут 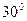 . Знайдіть об’єм паралелепіпеду,
. Знайдіть об’єм паралелепіпеду,
якщо його бічне ребро дорівнює 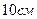 .
.
14. Основа піраміди - трикутник зі сторонами 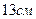 ,
, 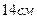 і
і 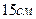 . Знайдіть площу перерізу,
. Знайдіть площу перерізу,
який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2 ,
рахуючи від вершин піраміди.
Завдання ІІІ-го рівня
15. Основа піраміди - рівнобедрений трикутник з бічною стороною 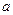 і кутом
і кутом 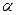 при основі.
при основі.
Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини
основи, а дві інші нахилені до неї під кутом 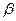 . Знайти об’єм піраміди.
. Знайти об’єм піраміди.
16. Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної
призми проведено переріз під кутом 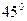 до площини основи. Знайти об’єм призми, якщо
до площини основи. Знайти об’єм призми, якщо
площа перерізу дорівнює 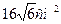 .
.
ПРИЗМА
1. прямая – бок. ребра  основанию
основанию
2. правил. – 1) прямая
2) в осн. прав. многоуг.
3. парал-д – в осн. парал-м
(все грани парал-мы)
4. свойства: 1)против.грани = и ║
2) диагонали ∩ в одной т.
и т.∩ делятся пополам
5. прямой парал-д – в осн. парал-м
бок. грани прямоугольники
6. прямоуг.пар-д – все грани прям-ки
7. свойства: 3) d2 = а2 + b2 + с2
8. куб – все грани квадраты








 A1 C1
A1 C1




 B1
B1
d c




 А С
А С
 b B
b B
a

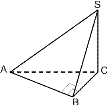
S



 УСЕЧЕННАЯ ПИРАМИДАA2
УСЕЧЕННАЯ ПИРАМИДАA2





 (А2В2С2)║ (А1В1С1) B2 А1В1С1А2В2С2 – усеч.пир.
(А2В2С2)║ (А1В1С1) B2 А1В1С1А2В2С2 – усеч.пир.
SА1В1С1 ~ SА2В2С2 А1 O1
В1

 МНОГОГРАННИКИ
МНОГОГРАННИКИ
 |  | ||
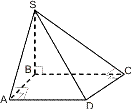
ПИРАМИДА
1. правил. – 1) в осн. прав. многоуг.
2) основание выс. в ц. многоуг.
2. тетраэдр – треуг. пирамида
3. правил. тетр. – все ребра =
1. ГДЕ РАСПОЛ. ОСН. ВЫСОТЫ ?
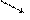

ц. впис ц. опис. в верш. др.
многоуг.
2. КАКОЙ МНОГОУГ. В ОСНОВАНИИ?
S
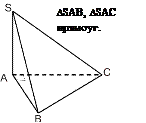 | |||||
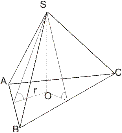 | 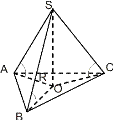 | ||||


B ПОДОБИЕ
Все прав. многог-ки
и шары подобны.

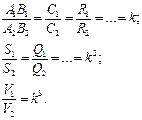
| <== предыдущая лекция | | | следующая лекция ==> |
| Українське художнє килимарство і ткацтво. | | | Декоратнвно-Прикладне мистецтво Київської Русі. |