
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Загальносвітові об'єднання
Дата добавления: 2014-12-06; просмотров: 833
|
|
1. Установите последовательность регуляции дыхания, начиная с процесса возникновения вдоха:
А) При вдохе легкие расширяются, в результате чего раздражаются рецепторы растяжения легких;
Б) При повышении содержания углекислого газа в крови, хеморецепторы сонных артерий и аорты посылают нервные импульсы в дыхательный центр
В) По чувствительным волокнам блуждающего нерва импульсы поступают в дыхательный центр продолговатого мозга, вызывая торможение центра вдоха и возбуждение центра выдоха
Г) Возбуждение передается в мотонейроны спинного мозга
Д) В результате происходит выдох
Е) По центробежным волокнам импульсы поступают к наружным межреберным мышцам и диафрагме, вызывая сокращение мышц.
Ж) Легкие спадаются, импульсы от рецепторов растяжения не поступают и центр выдоха отключается
З) В центре вдоха вновь возникает возбуждение.
Задание № 2
1). Найти длину высоты пирамиды, опущенной из вершины S.
2) Найти величину угла В треугольника АВС.
| № п/п | S | А | В | С |
| 1; 1; 2 | 2; 3; -1 | 2; -2; 4 | -1; 1; 3 | |
| 2; 1; 3 | 4; 5; -3 | 3; -2; 5 | 0; 1; 4 | |
| 1; 1; 1 | 2; 3; -2 | 3; -5; 5 | -1; 1; 2 | |
| 3; 3; 1 | 4; 5; -2 | 4; 0; 3 | -1; 3; 3 | |
| 2; -3; 4 | 5; 3; -5 | 3; -6; 6 | 0; -3; 5 | |
| 2; 1; 2 | 3; 3; -1 | 5; -8; 8 | 0; 1; 3 | |
| 1; 1; 3 | 2; 3; 0 | 2; -2; 5 | -5; 1; 6 | |
| 2; 2; 2 | 4; 6; -4 | 4; -4; 6 | 0; 2; 3 | |
| 0; 0; 1 | 2; 4; -5 | 1; -3; 3 | -4; 0; 3 | |
| 3; 3; 3 | 4; 5; 0 | 5; -3; 7 | -1; 3; 5 | |
| 1; 1; 0 | 3; 5; -6 | 3; -5; 4 | -3; 1; 2 | |
| 1; 0; 0 | 4; 6; -9 | 4; -9; 6 | -1; 0; 1 | |
| 0; 1; 0 | 3; 7; -9 | 1; -2; 2 | -6; 1; 3 | |
| 3; 2; 1 | 6; 8; -8 | 6; -7; 7 | -3; 2; 4 | |
| 1; 3; 1 | 2; 5; -2 | 4; -6; 7 | -5; 3; 4 | |
| 2; 4; 1 | 0; 4; 2 | 3; 6; -2 | 3; 1; 3 | |
| 1; 3; 2 | -3; 3; 4 | 2; 5; -1 | 2; 0; 4 | |
| 1; 0; 1 | -1; 0; 2 | 3; 4; -5 | 2; -3; 3 | |
| 2; 0; 0 | 0; 0; 1 | 3; 2; -3 | 4; -6; 4 | |
| 0; 0; 2 | 6; 0; 5 | 1; 2; -1 | 1; -3; 4 | |
| 0; 2; 0 | -2; 2; 1 | 3; 9; -9 | 1; -1; 2 | |
| 2; 0; 2 | 0; 0; 3 | 3; 2; -1 | 5; -9; 8 | |
| 1; 2; 1 | -3; 2; 3 | 3; 6; -5 | 2; -1; 3 | |
| 1; 2; 2 | -3; 2; 4 | 2; 4; -1 | 3; -4; 6 | |
| 2; 1; 2 | 0; 1; 3 | 4; 5; -4 | 4; -5; 6 | |
| -1; 0; -1 | -7; 0; 2 | 2; 6; -10 | 0; -3; 1 | |
| 0; -1; 1 | -6; -1; 4 | 1; 1; -2 | 3; -10; 7 | |
| 2; -1; -1 | 0; -1; 0 | 5; 5; -10 | 5; -10; 5 | |
| 1; -2; 0 | -3; -2; 2 | 3; 2; -6 | 3; -8; 4 | |
| -1; 0; 2 | -7; 0; 5 | 2; 6; -7 | 2; -9; 8 | |
| 1; -2; 1 | -3; -2; 2 | 6; 8; -14 | 2; -5; 3 | |
| 2; -1; 1 | 0; -1; 2 | 4; 3; -5 | 7; -16; 11 |
Вариант выбирается по первой букве фамилии студента соответственно
| А-1 | Б-2 | В-3 | Г-4 | Д-5 | Е-6 | Ж-7 | З-8 | И-9 | К-10 |
| Л-11 | М-12 | Н-13 | О-14 | П-15 | Р-16 | С-17 | Т-18 | У-19 | Ф-20 |
| Х-21 | Ц-22 | Ч-23 | Ш-24 | Щ-25 | Ю-26 | Я-27 |
Примеры решения некоторых задач контрольной работы
Пример № 1
Систему линейных алгебраических уравнений решить тремя способами:
1. методом Гаусса;
2. по формулам Крамера;
3. матричным способом.
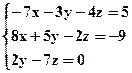
Решение:
1. Метод Гаусса – метод последовательного исключения неизвестных (решим им в матричном виде):
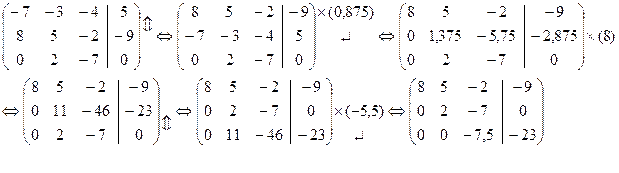
Вернёмся опять к системе: 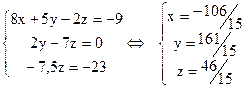
2. Найдём её решение с помощью формул Крамера.
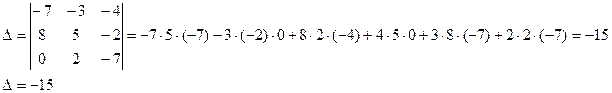
главный определитель отличен от нуля, следовательно, существует единственное решение системы.
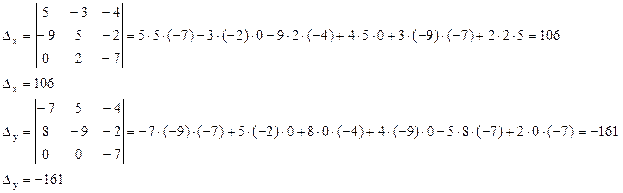
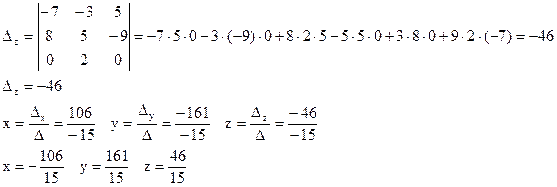
3. Матричный метод:
пусть 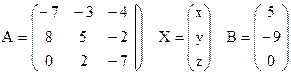 .
.
Тогда система линейных уравнений примет вид матричного уравнения: AX=B. Умножим слева обе части матричного уравнения на А-1–обратную матрицу для А: А-1AX= А-1B, где А-1A=Е – единичная матрица, то есть:
ЕX= А-1B, где ЕX=Х. Итак: X= А-1B. Ищем А-1 – обратную матрицу для А (если она существует) по формуле:
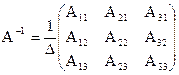
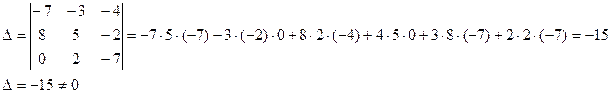
следовательно, обратная матрица существует.
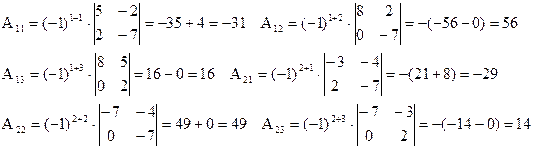
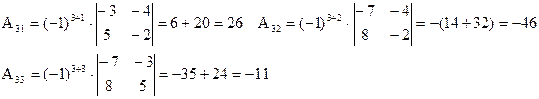
Итак, обратная матрица имеет вид:
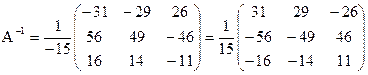
Ищем решение по формуле: X= А-1B.
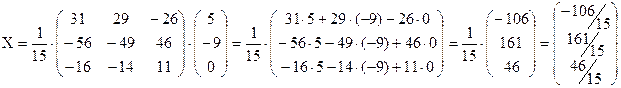
Итак, все три метода привели к единому ответу, что: 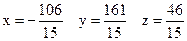 .
.
Ответ: (-106/15; 161/15; 46/15)

Вопросы к экзамену (зачету).
1.Правило вычисления определителей второго и третьего порядков.
Вычислить: 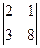 ;
; 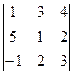

2. Свойства определителей.
3. Определение минора.
4. Определение алгебраического дополнения.
5. Определение матрицы, виды матриц.
6. Действия с матрицами.
7.Алгоритм нахождения обратной матрицы. Найти матрицу обратную для матрицы
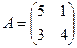
8.Решение систем линейных уравнений тремя способами:
1) методом Крамера
2)матричным способом
3)методом Гаусса
Решить систему:
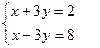
9. Определение вектора, координат вектора.
10. Линейные операции с векторами.
11.Скалярное произведение векторов (результат, определение, операция в координатной форме, геометрический смысл).
12.Векторное произведение векторов (результат, определение, операция в координатной форме, геометрический смысл).
13.Смешанное произведение векторов (результат, определение, операция в координатной форме, геометрический смысл).
14. Уравнения прямой на плоскости.
15. Уравнения плоскости.
16. Уравнения прямой в пространстве.
17. Взаимное расположение прямых и плоскостей.
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Економічна інтеграція. Економічні союзи | | | Форми зовнішньоекономічної діяльності. Зони спільного підприємництва. |