Определение сейсмических нагрузок для систем со многими степенями свободы. Подставляя (10-а) в (10) получаем
Подставляя (10-а) в (10) получаем
или с учетом (9)
Сопоставляя полученный результат с предпоследней лекцией
Теперь Введем коэффициент
Установим его физический смысл, просуммировав эти коэффициенты по всем формам:
Таким образом, Перепишем (11) в другой форме: Эта формула отличается от формулы линейного осциллятора коэффициентом η ik < 1. Тогда, повторяя все выкладки лекции о линейном осцилляторе, получим формулу СНиП: Сейсмическая нагрузка
где
Определение внутренних усилий Казалось бы, далее все просто, зная
где n – число учитываемых форм колебаний. Нормы требуют учета Алгоритм расчета Представленный алгоритм описывает последовательность расчета по нормам СНиП при ручном расчете, а также при расчете на ЭВМ практически по любой программе. · Определяются частоты и формы колебаний для выбранных n форм. · Вычисляются параметры · Для каждой i-й частоты определяются сейсмические силы · Производится статический расчет для n вариантов загружений от найденных сил · Определяются расчетные усилия Результаты расчетов · Выводятся сейсмические силы и формы колебаний для каждой частоты собственных колебаний. · Выводятся на экран расчетные усилия M, Q, N по первому варианту загружения, причем, поскольку все расчетные усилия только положительны, не следует ожидать равновесия усилий в узлах. Расчет на воздействие акселерограмм Основан на использовании записей ускорений основания (акселерограмм) при землетрясениях, наиболее опасных для рассматриваемых сооружений, а также синтезированных акселерограмм, полученных путем обработки записей сильных землетрясений. СНиП предусматривает обязательный расчет по нормам для всех зданий и сооружений, но вместе с тем для ответственных и высоких, выше 16 этажей зданий и сооружений, предписывается расчет на воздействие акселерограмм. 1) Первый подход – непосредственное вычисление сейсмических сил. Теоретически, по формуле (12) Где 2) Уравнения движения представим в виде
Это система дифференциальных уравнений первого порядка в нормальной форме. Рассмотрим процедуру метода Рунге-Кутта вначале на простейшем случае – уравнении первого порядка
Это метод Эйлера, или метод Рунге-Кутта первого порядка, т.к. он соответствует разложению кривой q(t) в ряд Тэйлора по степеням ∆ t и удержания первого линейного члена ряда. Погрешность имеет порядок ∆ t2, что записывается как О (∆ t2). По формуле (15) находим следующую точку, вычисляя один раз функцию Мы в программе используем метод Рунге-Кутта четвертого порядка, в котором переход от tk к tk+1 выполняется по формулам
Где При этом требуется четыре раза вычислять функцию F.
Геометрически формула (16) выражает переход от точки k к точке k+1 с помощью секущей, проведенной с крутизной f (тангенс угла наклона), которая получена как среднее из f1 – f4, вычисленных в 4-х точках 1 – 4. Погрешность формул (16 ) О (∆ т5), т.е. значительно меньше, чем у формулы (15). Если вместо одного уравнения система уравнений первого порядка, то Таким образом, в каждый момент времени получаем qi(t), а затем по формуле (10-б) Существуют и другие методы (так называемые методы линейного ускорения) – методы Ньюмарка, Вилсона и т.д. – см. рекомендованные книги Александрова, Bathe, Wilson. Итак, подводим итог: дана система уравнений
Где Z – вектор перемещений. Считаем, что вектор
Здесь i, j, k – орты координатных осей. С помощью метода модальной суперпозиции получаем разделение уравнений
На каждом шаге по времени для каждой формы колебаний находим сейсмические силы для каждой массы по формуле (10-б), после нахождения
Выбор шага по времени Метод Рунге-Кутта условно устойчивый, т.е. его точность зависит от величины шага по времени. Рекомендуется Алгоритм решения · Формируется матрицы · Вычисляются частоты и формы свободных колебаний. · Определяются обобщенные массы Mi и обобщенные нагрузки Qi(t). · Решаются уравнения (15) и для всех выбранных форм колебаний находятся обобщенные координаты qi для каждого временного шага. · Для каждого временного шага вычисляется вектор · Для каждого временного шага определяются внутренние усилия · На каждом временном шаге определяются нормы динамических перемещений · На момент времени tk, когда · Строится выборка максимальных значений усилий по всем временным шагам для каждого сечения, строятся эпюры усилий. Равновесия в узлах ожидать не следует, т.к. в разных сечениях максимальное усилие появляется в разные моменты времени.
|

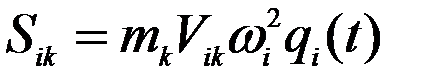 (10-б)
(10-б)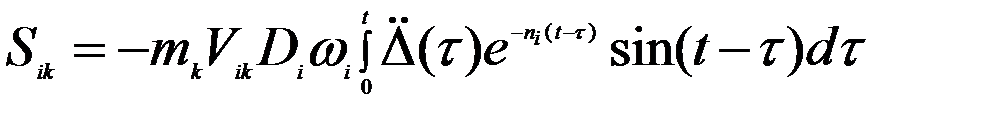
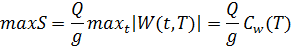
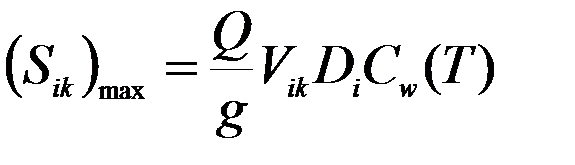
 :
: 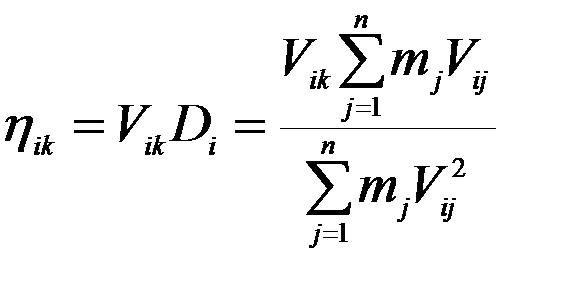 . (11)
. (11) .
.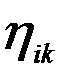 - нормированный коэффициент формы колебаний – это коэффициент, определяющий вклад смещения к-й массы, происходящий по i-й форме, в суммарное смещение.
- нормированный коэффициент формы колебаний – это коэффициент, определяющий вклад смещения к-й массы, происходящий по i-й форме, в суммарное смещение.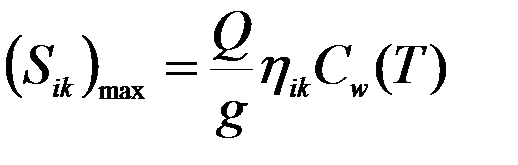 (12)
(12)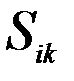 приложенная в точке k, соответствующая i-му тону колебаний, определяется формулами
приложенная в точке k, соответствующая i-му тону колебаний, определяется формулами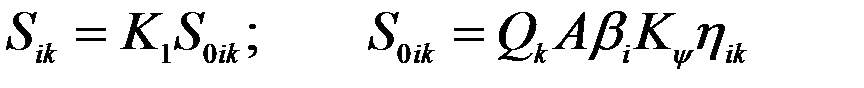 , (13)
, (13)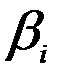 коэффициент динамичности, соответствующий i-му тону колебаний.
коэффициент динамичности, соответствующий i-му тону колебаний.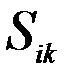 , можно построить эпюры внутренних усилий Ni (M, Q, N) однако максимальные значения сейсмических сил по формулам (13) достигаются в различные моменты времени. Задача эта непростая. В нормах принято среднеквадратичное значение усилий
, можно построить эпюры внутренних усилий Ni (M, Q, N) однако максимальные значения сейсмических сил по формулам (13) достигаются в различные моменты времени. Задача эта непростая. В нормах принято среднеквадратичное значение усилий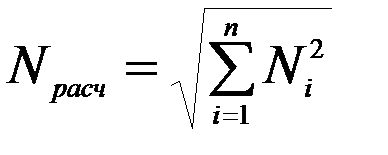 , (14)
, (14) и только 1 форму, если
и только 1 форму, если  . Для ответственных зданий необходимо учитывать
. Для ответственных зданий необходимо учитывать 

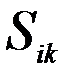 , приложенные к k-й массе и эти силы считаются как внешние силы для i-го варианта загружения.
, приложенные к k-й массе и эти силы считаются как внешние силы для i-го варианта загружения.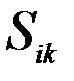 .
.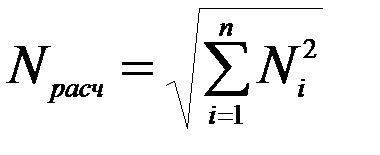 .
.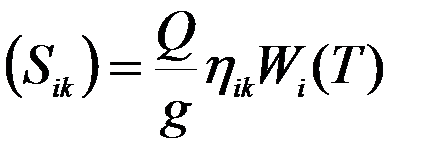 ,
,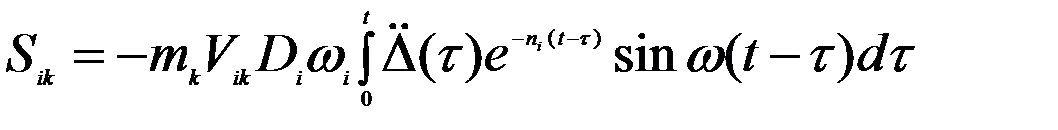 Вычисление интеграла Дюамеля можно произвести с помощью различных алгоритмов, простейший из них описан в книге Александрова и др. на стр. 53. Там функция внешнего воздействия представляется в виде кусочно-линейной, на каждом шаге интегрирования определяются перемещения и скорости, которые служат начальными для следующего шага.
Вычисление интеграла Дюамеля можно произвести с помощью различных алгоритмов, простейший из них описан в книге Александрова и др. на стр. 53. Там функция внешнего воздействия представляется в виде кусочно-линейной, на каждом шаге интегрирования определяются перемещения и скорости, которые служат начальными для следующего шага. Второй подход – численное интегрирование уравнений движения (7-а). Разработано множество методов, среди которых можно назвать методы Ньюмарка, Вилсона, Хаболта и другие. Здесь мы подробно рассмотрим метод Рунге-Кутта, который реализован в программе RADIUS, далее применяемой при решении конкретных задач сейсмического расчета.
Второй подход – численное интегрирование уравнений движения (7-а). Разработано множество методов, среди которых можно назвать методы Ньюмарка, Вилсона, Хаболта и другие. Здесь мы подробно рассмотрим метод Рунге-Кутта, который реализован в программе RADIUS, далее применяемой при решении конкретных задач сейсмического расчета.
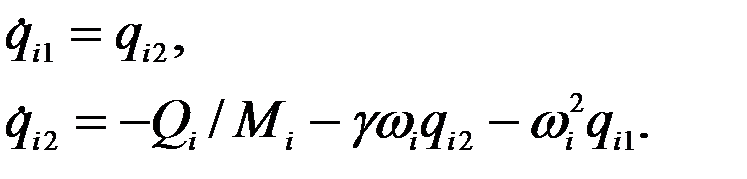
 , тогда, в соответствии с рисунком
, тогда, в соответствии с рисунком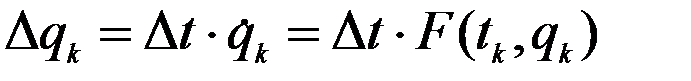
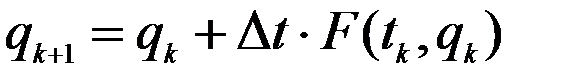 (15)
(15)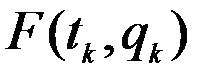 . Недостаток – с увеличением числа шагов быстро накапливается погрешность e1.
. Недостаток – с увеличением числа шагов быстро накапливается погрешность e1. (16)
(16)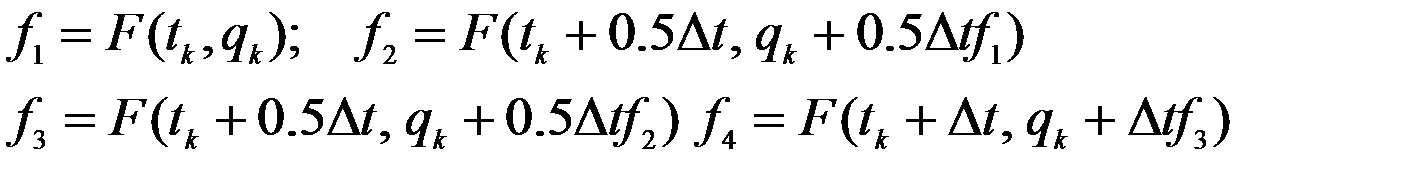 .
.
 - векторы.
- векторы.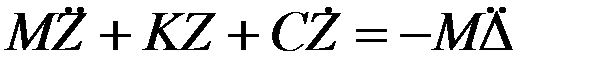
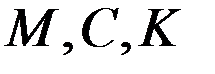 , матрицы масс, демпфирования, жесткости,
, матрицы масс, демпфирования, жесткости, задан в глобальной системе координат. Тогда осевые компоненты
задан в глобальной системе координат. Тогда осевые компоненты (17)
(17)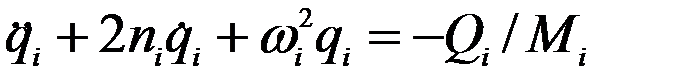
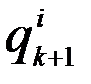 методом Рунге-Кутта.
методом Рунге-Кутта.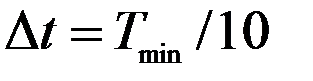 , где
, где 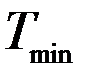 - минимальный период учитываемых форм.
- минимальный период учитываемых форм. .
. .
.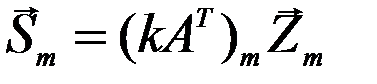 , где
, где  - вектор перемещений m-го элемента.
- вектор перемещений m-го элемента.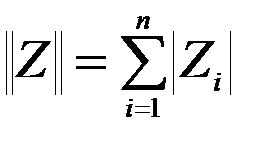 - сумма модулей компонент перемещений.
- сумма модулей компонент перемещений. , выводятся результаты расчета - перемещения и усилия.
, выводятся результаты расчета - перемещения и усилия.


