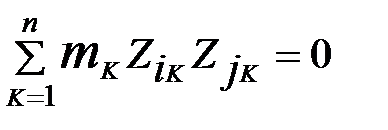Нормативный расчет трехэтажного здания
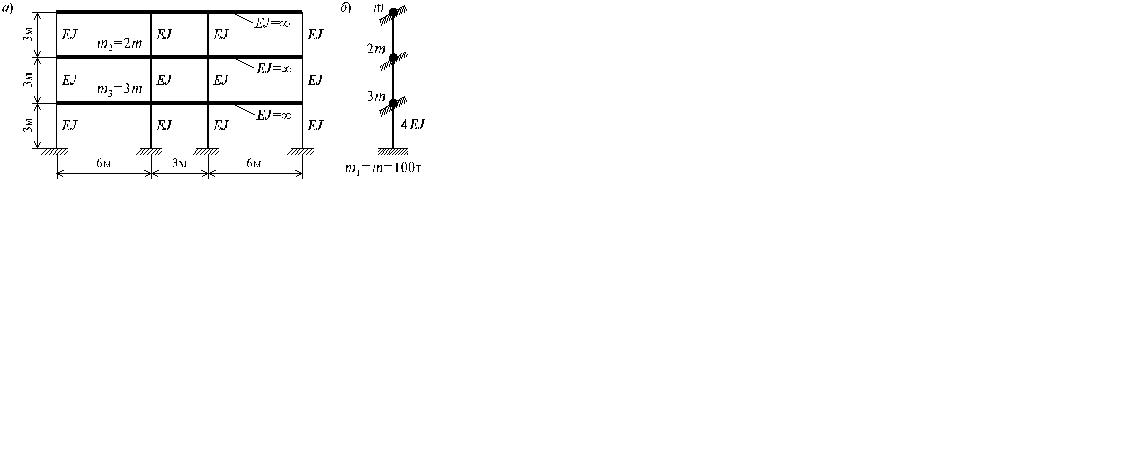
В качестве примера расчета здания по нормативному методу рассмотрим трехпролетное трехэтажное здание с монолитными безбалочными перекрытиями (Рис. а).
Конструктивная и расчетная схемы здания Колонны - железобетонные, монолитные, сечением 0, 3´ 0, 3 м. Расчетная сейсмичность района строительства - 9 баллов; грунты глинистые (III категории). Будем считать, что изгибная жесткость безбалочного перекрытия и покрытия значительно больше суммарной изгибной жесткости колонн, и поэтому в качестве расчетной схемы примем консольный стержень с узловыми заделками, (Рис. б). Для динамического расчета данной системы используем метод перемещений. Основная система метода перемещений и единичные эпюры изгибающих моментов приведены на следующем рис.
Основная система и единичные эпюры изгибающих моментов метода перемещений
Составляя уравнения движения, имеем:
Определение частот и форм собственных колебаний Решение системы уравнений (18) ищем в виде:
где а 1 , а 2 , а 3 - амплитудные коэффициенты; w - частота колебаний. Подставляя (18а) в (18), получаем систему однородных алгебраических уравнений.
Вычисляя коэффициенты системы канонических уравнений метода перемещений ri к, имеем
где r = 4 i /3 = 16 EJ /9. Введем параметр l = w2 m / r. Тогда с учетом принятых обозначений система уравнений (19) может быть представлена в виде:
Как обычно, для вычисления собственных значений системы однородных уравнений (21) используем условие равенства нулю определителя, составленного из коэффициентов этой системы:
Раскрывая этот определитель, получаем кубическое уравнение относительно искомого параметра l: 6 l3 - 16 l2 + 10 l - 1 = 0. (23) Корни кубического уравнения (23), которые, как это известно из общего курса динамики сооружений, являются действительными положительными числами, могут быть вычислены по стандартным программам на ЭВМ или калькуляторах. Здесь для иллюстрации приведем один из способов нахождения корней уравнения (23), приспособленный для ручного счета. Для нахождения первого корня l1 уравнения (23) применяем итерационный метод. Первое приближение
Подставляя это значение l = Для второй итерации принимаем Продолжая итерационный процесс, в пятом приближении получаем Понятно, что продолжая этот итерационный процесс, можно обеспечить сколь угодно высокую точность вычисления l1 . Принимая l = 0, 123, разделим уравнение (3.18) на множитель (l - 0, 123). В таком случае получаем квадратное уравнение 6 l2 - 15, 262 l + 8, 123 = 0, корни которого легко вычисляются: l2 = 0, 758; l3 = 1, 786. Для проверки правильности вычисления корней уравнения (23), приводим определитель (22) к виду
где Е - единичная диагональная матрица. Здесь должно выполняться условие
- сумма корней уравнения (23); SD = 1 + 1 + 2/3 = 2, 667 - след матрицы D, равный сумме диагональных элементов этой матрицы. Возвращаясь к введенным выше обозначениям параметров l и r, вычисляем частоты собственных колебаний по формуле
где E = 2, 7× 107 кН× м2 ; Имеем: w1 = 6, 313 сек-1; w2 = 15, 67 сек-1; w3 = 24, 05 сек-1. Отсюда находим периоды колебаний: Ti = 2 p /w i : T 1 = 0, 995 сек; T 2 = 0, 401 сек; T 3 = 0, 261 сек; Определение форм собственных колебаний Определение форм собственных колебаний производим по методике, известной из общего курса динамики сооружений Находим:
где Проверяем ортогональность форм собственных колебаний Например, для первой и второй форм имеем: m (1× 1× 1 + 2× 0, 877× 0, 242 - 3× 0, 538× 0, 883) = 0, 0007» 0. Аналогично проверяется ортогональность первой и третьей, второй и третьей форм.
|

 m1=m=100 т
m1=m=100 т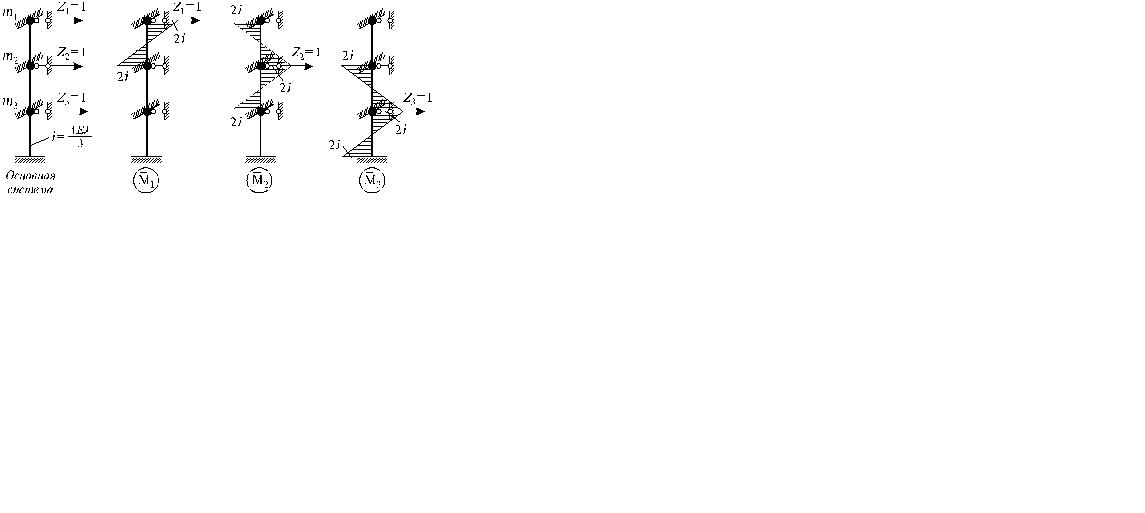
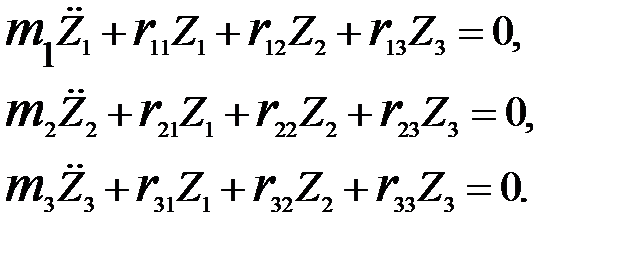 (18)
(18)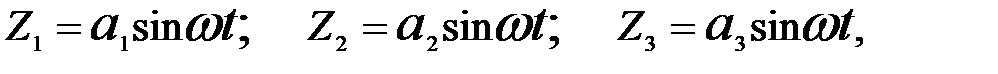 (18а)
(18а)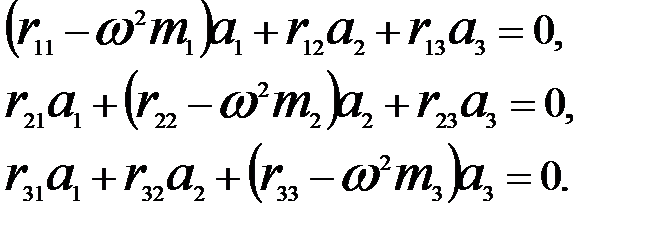 (19)
(19) (20)
(20)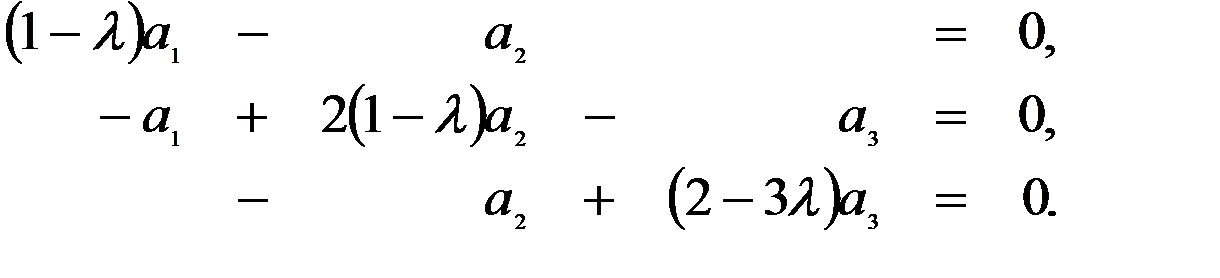 (21)
(21) . (22)
. (22) принимаем в виде отношения последних коэффициентов уравнения (23)
принимаем в виде отношения последних коэффициентов уравнения (23) = 0, 15. В этом случае имеем А (2) = 0, 160. Очевидно, истинное значение корня l1 заключено в интервале 0, 1 £ l1 £ 0, 15.
= 0, 15. В этом случае имеем А (2) = 0, 160. Очевидно, истинное значение корня l1 заключено в интервале 0, 1 £ l1 £ 0, 15.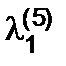 = 0, 123; при этом А (5) = -0, 001.
= 0, 123; при этом А (5) = -0, 001.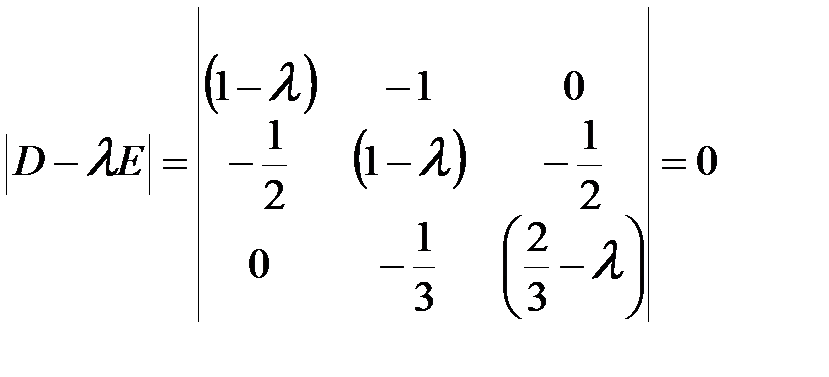 ,
,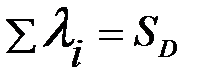 , где
, где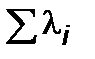 = 0, 123 + 0, 758 + 1, 786 = 2, 667
= 0, 123 + 0, 758 + 1, 786 = 2, 667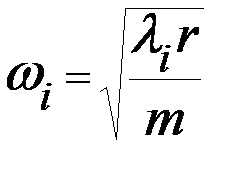 , (24)
, (24) м4 .
м4 . , (25)
, (25)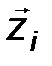 - векторы, определяющие i -ую форму колебаний.
- векторы, определяющие i -ую форму колебаний.