Крок 1. Покажемо, що 


Крок 2. Покажемо, що 
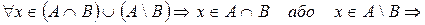

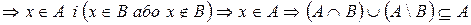
За результатами виконання кроків 1 і 2 робимо висновок, що  .
.
Завдання 8. Довести справедливість тотожності  .
.
Доведення.
Нехай  , тоді
, тоді  або
або  . Якщо
. Якщо  , то
, то  належить об’єднанню
належить об’єднанню  з будь-якою множиною, тобто
з будь-якою множиною, тобто  і
і  , отже,
, отже,  є елементом перетину множин
є елементом перетину множин  і
і  , тобто
, тобто  .
.
Якщо  , то
, то  і
і 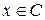 , отже,
, отже,  і
і  , тобто і у цьому випадку
, тобто і у цьому випадку  є елементом перетину тих же множин.
є елементом перетину тих же множин.
Таким чином, доведено  . Аналогічно доводиться і співвідношення
. Аналогічно доводиться і співвідношення 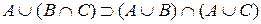 . Відповідно до визначення рівності множин приходимо до необхідної тотожності
. Відповідно до визначення рівності множин приходимо до необхідної тотожності  .
.
Завдання 9. Довести справедливість співвідношення  .
.
Доведення.
Співвідношення  доводиться наступними перетвореннями з використанням тотожностей алгебри множин:
доводиться наступними перетвореннями з використанням тотожностей алгебри множин:
 .
.
Завдання 10. Указати всі підмножини множини  .
.





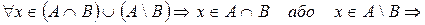

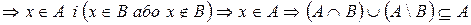
 .
. .
. , тоді
, тоді  або
або  . Якщо
. Якщо  належить об’єднанню
належить об’єднанню  з будь-якою множиною, тобто
з будь-якою множиною, тобто  і
і  , отже,
, отже,  і
і  , тобто
, тобто  .
. і
і 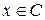 , отже,
, отже,  . Аналогічно доводиться і співвідношення
. Аналогічно доводиться і співвідношення 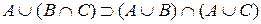 . Відповідно до визначення рівності множин приходимо до необхідної тотожності
. Відповідно до визначення рівності множин приходимо до необхідної тотожності  .
. .
. .
.


