Представление сигнала посредством выборок. Теорема В.А.Котельникова
Как мы уже говорили, при оцифровывании сигнала делаются выборки, при этом, для получения значения сигнала применяют дискретизацию и квантование. В ряде случаев, моменты взятия выборок устанавливаются на оси времени случайно, при этом информация о форме сигнала теряется. По случайным выборкам мы можем определить только плотность распределения вероятностей. Таким образом, случайные выборки дают нам статистическую информацию о величине входного сигнала. Это означает, что таким способом мы можем измерить среднеквадратическое и пиковое значения входного сигнала, определить диапазон принимаемых им значений, но форму сигнала и его спектр мы определить не сможем. Во многих случаях взятие выборок сигнала осуществляется в равноотстоящие моменты времени. Тогда важно решить вопрос о том, как много выборок надо брать в единицу времени, чтобы иметь возможность достаточно полно описать непрерывный по времени сигнал. Ответ на этот вопрос даёт теорема В.А.Котельникова. В иностранной технической литературе Вы можете столкнуться с другим названием этой теоремы, которая трактуется как теорема Шеннона о выборках. В этой теореме утверждается, что для восстановления без ошибок исходного сигнала по его выборочным значениям, взятым через равные промежутки времени, частота взятия выборок должна более, чем вдвое превосходить частоту самой высокочастотной составляющей, присутствующей в непрерывном входном сигнале. Строго говоря, текст теоремы В.А.Котельникова звучит следующим образом: Если функция x(t), удовлетворяющая условиям Дирихле и обладающая спектром с граничной частотой, дискретизирована циклически, с периодом, то она может быть восстановлена по этой совокупности ее мгновенных значений без погрешности. (сек) (Гц). Условие Дирихле означает, что функция ограничена, кусочно непрерывна и имеет ограниченное число экстремумов. Особенностью сигнала, дискретизированного в соответствие с теоремой Котельникова является то, что он может быть восстановлен с помощью фильтра нижних частот. Следовательно, если дискретизированный с шагом
Рис.. Схема дискретизации и восстановления сигнала
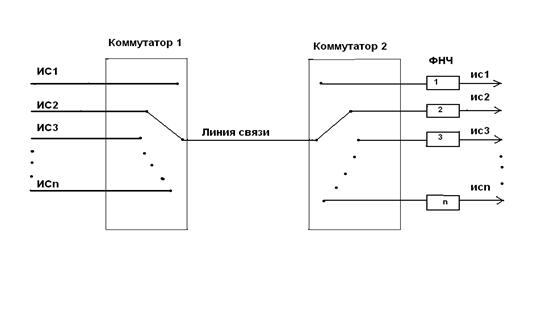
Рассмотрим передачу нескольких сигналов по одной линии связи, для этого их необходимо дискретизировать. Эта операция реализуется с помощью коммутатора, затем информация передаётся по линии связи и далее, зная частоту работы коммутатора, мы можем восстановить её на другом конце линии связи (рис.). Частота опроса коммутатора должна быть Теорема Котельникова позволяет производить преобразования аналогового сигнала в цифровой, необходимый для его дальнейшей обработки с помощью средств вычислительной техники. Выбор шага дискретизации по Котельникову гарантирует сохранность в дискретном представлении сигнала, всей информации о его спектральном составе. Для преобразования аналогового сигнала в цифровой используют АЦП. Частота дискретизации АЦП в соответствии с теоремой Котельникова
Рис. Передача информации по одной линии связи
При обратном цифро-аналоговом преобразовании роль фильтра нижних частот выполняет микросхема ЦАП. Число разрядов АЦП и ЦАП преобразования определяют точность передачи амплитуды сигнала, т.к. определяют уровни дискретизации амплитуды сигнала. Таким образом, в компьютер поступает информация о сигнале в виде точек.
Рис. Дискретизация сигнала после АЦП
Обычно микросхемы АЦП выпускаются в одном корпусе с коммутаторами на n каналов. При этом в паспорте регламентируется частота опроса, которая может использоваться как для опроса n каналов, так и для опроса 1 канала. Ввод в компьютер информации производится через последовательный порт, например в стандарте RS-232. В связи с этим проектант в каждом конкретном случае принимает решение об использовании нужной микросхемы с необходимым числом каналов, необходимой частотой опроса и числом разрядов АЦП преобразования. Следует отметить, что дополнять измерительную схему фильтром нижних частот не всегда удобно, кроме того, наличие такого фильтра приводит к фазовым искажениям сигнала. От этих недостатков свободно восстановление сигнала методом простейшей интерполяции.
|

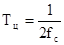 сигнал х(t)дискр. подать на вход идеального фильтра с верхней границей пропускания
сигнал х(t)дискр. подать на вход идеального фильтра с верхней границей пропускания 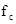 , то на выходе получается восстановленный без погрешностей непрерывный сигнал х(t) (Рис)
, то на выходе получается восстановленный без погрешностей непрерывный сигнал х(t) (Рис)
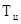 n, где n — число измерительных преобразователей.
n, где n — число измерительных преобразователей.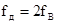 , где
, где 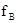 — верхняя граничная частота сигнала.
— верхняя граничная частота сигнала.