Полные динамические характеристики системы с сосредоточенными параметрами

В соответствии с ГОСТ 8.256 к полным динамическим характеристикам системы с сосредоточенными параметрами относятся: дифференциальное уравнение, импульсная характеристика, переходная характеристика, передаточная функция, совокупность амплитудной и фазочастотной характеристик. В связи с удобством реализации в автоматике наибольшее распространение получил метод измерения амплитудной и фазочастотной характеристик.

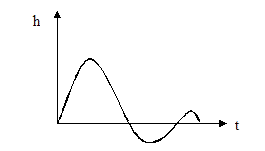
Дифференциальное уравнение и передаточная функция рассматривались ранее, рассмотрим остальные характеристики. Что же такое переходная характеристика? Пусть на вход звена подаётся ступенчатое воздействие . Выходная величина звена определяется видом его дифференциального уравнения. Отношение 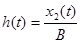выходной величины звена при входном воздействии в виде ступенчатой функции к ординате этой функции при нулевых начальных условиях и отсутствие возмущающих воздействий называется переходной характеристикой звена. Часто в качестве переходной функции рассматривают не указанное отношение, а непосредственно выходную величину, но при условии, что входное ступенчатое воздействие является единичным, т.е. В=1. Практически воздействие в виде ступенчатой функции имеет место при подаче постоянного напряжения на вход какого либо устройства или при резком повороте датчика угла в автоматической системе слежения за углом и т.п. Импульсная функция и реакция системы на воздействие изображены на втором рисунке.

 

 

 

Частотными характеристиками называются зависимости, связывающие выходную и входную величины звена в установившемся режиме, при условии, что входная величина изменяется по гармоническому закону . Тогда в установившемся режиме выходная величина

 

 

 

Отношение амплитуд входной и выходной величин и угол сдвига y являются функциями частоты w. Вид этих функций определяется дифференциальным уравнением звена. Представим, что звено описывается линейным дифференциальным уравнением второго порядка.

Используем символическую запись гармонических функций, т.е. представление об условной замене гармонической функции комплексным числом модуль которого равен амплитуде, а аргумент – фазе гармонической функции. При этом функция x₂(t) равна мнимой части её комплексного изображения .

Функции

и

будут иметь комплексные изображения

и

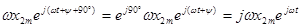Аналогично комплексные изображения функций ; ; будут равны соответственно ; ; . Подставляя полученные комплексные изображения в дифференциальное уравнение звена, находим:

или

Это комплексное число, модуль которого равен отношению амплитуд выходной и входной гармонических функций, а аргумент – сдвигу фаз выходной функции относительно входной, называется частотной передаточной функцией. Модуль частотной передаточной функции

называется амплитудно – частотной характеристикой (АЧХ) звена, а аргумент частотной передаточной функции

называется фазовой частотной характеристикой (ФЧХ) звена.