Уравнение второго порядка
Системы с одной степенью свободы, это системы с сосредоточенными параметрами. Для них характерно наличие масс, которые считаются недеформируемыми и сосредоточенными в конечном числе точек. Системы с бесконечно большим числом степеней свободы называются системами с распределенными параметрами. К ним относятся мембраны, струны, стержни и другие упругие тела. Подвижная система с одной степенью свободы, т.е. система с сосредоточенными параметрами может быть описана дифференциальным уравнением 2-го порядка. К числу приборов описываемых такими уравнениями относятся: гироскопические вертикали, пружинные акселерометры с жидкостным демпфированием, гальванометры различных типов. Для описания процессов, происходящих в системах с распределенными параметрами, применяют дифференциальные уравнения в частных производных с переменными коэффициентами. Уравнение моментов системы с сосредоточенными параметрами рассмотрим на примере маятникового акселерометра.
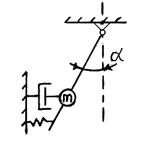
Рис. Схема маятникового акселерометра Без учёта сил сухого трения уравнение имеет вид:
где J – момент инерции подвижной системы; К¶ - коэффициент углового демпфирования; Сж – угловая жесткость, а – угол отклонения маятника, x – перемещение объекта, на котором установлен акселерометр, вдоль оси его чувствительности. Q – параметр, определяющий возмущающие силы. В том случае, если действует постоянное ускорение, то Q=ml, где l – расстояние от оси подвеса до центра тяжести маятника. При действии ускорения по гармоническому закону Q=mlsin(wt+j). Где j - сдвиг фазы между возмущающим воздействием и отклонением маятника. Следует обратить внимание на то, что размерность правой части уравнения соответствует размерности левой его части. Рассуждения касаются именно маятниковых акселерометров т.е. приборов у которых чувствительная масса расположена на маятнике. Все дальнейшие выкладки будут справедливы и для осевых акселерометров у которых подвижная масса отклоняется возвратно – поступательно вдоль оси.
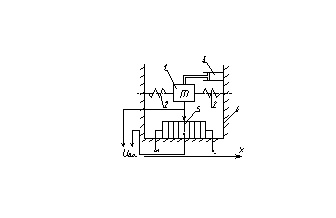
Здесь 1-подвижная масса, 2-пружины, 3-демпфер, 4-корпус, 5-потенциометр. Однако в этом случае в уравнении следует произвести замену некоторых специфических составляющих величин, относящихся к угловому движению. При этом, уравнение будет иметь вид:
Здесь m – масса маятника, a - его перемещение, К¶ - коэффициент линейного демпфирования; Сж – жесткость пружины. При постоянном ускорении Q=m, при изменяющемся по гармоническому закону Q=msin(wt+j). Уравнение второго порядка необходимо для расчёта АЧХ и ФЧХ систем. В этом случае мы задаём амплитуду сигнала и рассчитываем характеристики при каждом значении w. Если принять угол a за выходной сигнал, то передаточная функция прибора будет:
Рассмотрим реакцию системы на ступенчатое воздействие x=А 1(t) при нулевых начальных условиях (t = 0, Характеристическое уравнение системы т.е. уравнение при отсутствие возмущающих сил:
Это уравнение можно переписать: р2 + 2bр +w02 = 0 где Параметр w0 определяет круговую частоту собственных не демпфированных колебаний системы. Учитывая, что на собственную частоту не демпфированных колебаний углового маятникового акселерометра, расположенного вертикально, кроме жёсткости пружины влияет также составляющая силы тяжести, выражение для w0 должно быть переписано в виде
Отметим, что слагаемое mgl, как правило, существенно меньше жёсткости пружины. Далее введем безразмерный коэффициент, называемый степенью успокоения:
Величина степени успокоения существенно влияет на формы переходного процесса и частотных характеристик. Для определения переходной функции вначале решают характеристическое уравнение и находят его корни p1 и p2. Характеристическое уравнение запишем в виде P2 + 2 xw0 P + w02 = 0. Корни уравнения определим из выражения р1, 2 = - xw0 ± w0 Выражение для амплитуды колебаний системы, имеет вид:
В общем случае вид переходного процесса системы 2-го порядка зависит от характера корней р1, р2 здесь могут быть три случая:
|


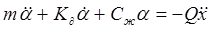
 (22)
(22)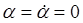 ).
).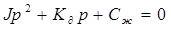
 .
.

 (23)
(23)



