Р1 ¹ р2 . Корни не равны и действительны
Этот случай соответствует x> 1.
При этом переходная функция при p1¹ p2:
Разделив (24) на установившееся значение
где t - безразмерное время. Переходный процесс в системе второго порядка при x> 1 и при нулевых начальных условиях имеет апериодический характер. Динамическая ошибка системы равна
Теперь, если левую часть уравнения приравнять допустимой динамической ошибке D и решить уравнение относительно t, то получим безразмерную длительность переходного процесса. Однако это уравнение не имеет явного решения относительно t, а возможно лишь численное решение задачи. На рисунке показаны кривые переходных процессов в системе 2-го порядка. В таблице приведены значения безразмерной длительности переходного процесса
Действительная длительность переходного процесса равна найденному из таблицы значению
Рис.. Формы переходных процессов кривая при x> 1; 2.— кривая при x=1; 3 — кривая при x< 1.
9.3.2 Корни равны друг другу (р1 = р2). Этот случай соответствует x=1. При этом корни: р1 = р2 = -w0. Переходная функция при подаче ступенчатого воздействия имеет вид:
Установившееся значение j(t) определяется при t = ¥:
Разделив j(t) на j(¥) получим безразмерную переходную функцию:
где t = w0t – безразмерное время. Переходный процесс Динамическая ошибка: D = 1- e = (1+ t)е-t. 9.3.3 Корни характеристического уравнения неравные и комплексные (р1¹ р2, x< 1) В этом случае существует некоторое оптимальное значение x, при котором длительность переходного процесса получается минимальной. Корни характеристического уравнения в данном случае равны:
Если подставить эти выражения в уравнение переходной функции (24) и совершить переход от комплексных выражений к тригонометрическим, можно получить переходную функцию в виде:
Переходные процессы при x< 1 имеют колебательный характер. Из последнего уравнения определяются основные показатели переходного процесса. Круговая частота колебаний демпфированной системы:
При x = 0 система является недемпфированной, при этом Частота колебаний в Герцах:
Период колебаний:
где T0 = Декремент затухания d, равный отношению абсолютных значений двух максимальных отклонений за два последовательных полупериода:
где j0, j1, j2 и j¥ - значения функции соответственно при t = 0, t = T/2, t = T, t = ¥. Подставляя последовательно в уравнение (25) значения t = 0, t = T/2 и t = ¥ находим:
Подставляя (27) в (26) определим декремент затухания:
иногда пользуются обратной величиной
Логарифмический декремент затухания:
По формулам (28) и (29) вычислены d, s, D, которые сведены в таблицу:
При колебательном процессе аналитическое определение безразмерной длительности переходного процесса tпп не представляется возможным т.к. кривая переходного процесса пересекает зону допустимых динамических ошибок ±D несколько раз и поэтому tпп приходится определять графически (кривая 3 на рисунке). Действительная длительность переходного процесса равна Следовательно, увеличение собственной частоты не демпфированных колебаний приводит к уменьшению длительности переходного процесса.
|
(24)
, выражая р1 и р2 через w0 и x в соответствии с (23) и заменяя w0t=t, получим выражение переходной функции в безразмерной форме
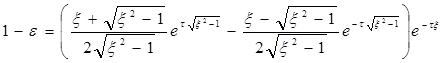
, вычисленные по уравнению для динамической ошибки системы при x> 1 и D=0, 1.
= f(t) также является апериодическим (кривая 2 на рис.).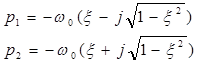
(25)
. Следовательно, параметр w0 представляет собой недемпфированную частоту собственных колебаний. С увеличением x частота w уменьшается от w = w0 (при x = 0) до w = 0 (при x=1).
, где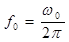 
.
– период колебаний недемпфированной системы. С увеличением x период T увеличивается, стремясь к ¥ при x = 1.
(26)
(27)
,
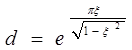— это есть перерегулирование, оно определяет относительную величину разности между первым максимумом переходного процесса и его установившимся значением: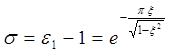
(28)
. (29)
