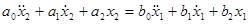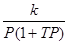Динамические звенья

Для теоретического исследования работы приборов и систем необходима оценка каждого их элемента не по устройству и назначению, а в зависимости от вида описывающего его дифференциального уравнения. В этом смысле нет никакого отличия между механическими и электрическими устройствами, например

или

Первое из них механическое- описывается уравнением

Где a и b углы на входе и выходе устройства, J – момент инерции диска, С – коэффициент упругости пружины.

Второе устройство электрическое описывается уравнением

где u₁ и u₂ напряжения на входе и выходе электрической цепи L и С – её индуктивность и ёмкость.

Для устройств, дифференциальное уравнение которых имеет порядок не выше второго, а это как правило системы с сосредоточенными параметрами(в механике системы с одной степенью свободы) можно записать

где x₁ – входная, а x₂ – выходная величины, которые обычно отсчитываются от их значений, соответствующих положению равновесия. В частном случае, когда a₁=b₀=b₁=0 из этого уравнения получается уравнение устройств, показанных на рисунках.

В правой части уравнения расположены возмущающие силы, а в левой реакция на возмущения со стороны измерительной системы

Динамическим звеном называется устройство любой физической природы и любой конструкции, описываемое дифференциальным уравнением определённого вида. Понятие динамического звена позволяет рассматривать характеристики различных устройств независимо от их конструкции. Здесь и далее рассматриваются только линейные устройства с постоянными параметрами, которым соответствует линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Для классификации звеньев вместо дифференциального уравнения можно использовать передаточную функцию.

Передаточной функцией динамического звена называется отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях. Передаточная функция определяется дифференциальным уравнением звена и наоборот. Для получения передаточной функции из дифференциального уравнения нужно заменить в нём выходную и входную величины x₂(t) и x₁(t) их операторными изображениями X₂(P) и X₁(P) а вместо первой, второй и других производных этих величин записать указанные изображения, умноженные на Р, Р² и т.д., где Р аргумент операторного преобразования функции времени. Из полученного в результате такой замены операторного уравнения определяется передаточная функция

Например, для последнего уравнения получим

 

откуда

Из определения передаточной функции следует, что изображение выходной величины звена равно

Любые приборные и автоматические системы могут быть разбиты на отдельные звенья, каждое из которых описывается дифференциальным уравнением не выше второго порядка. При этом один реальный элемент не обязательно сводится к одному звену, возможны случаи, когда один элемент приходится заменять сочетанием двух и более звеньев, каждое из которых описывается уравнением не выше второго порядка. Типовые звенья делятся на три большие группы: позиционные, интегрирующие и дифференцирующие.

 

Типовые звенья

 

№ п/п		Тип звена	Передат. ф-я
	Позиционные	Безынерционное	k
	Апериодическое 1-го порядка
	Апериодическое 2-го порядка
	Колебательное
	Консервативное
	Интегри- рующие	Идеальное интегрирующее
	Интегрирующее с замедлением
	Дифференцирующие	Идеальное дифференцирующее	kP
	Дифференцирующее с замедлением

 

 

Позиционными (статическими) называются звенья, в которых в установившемся режиме существует линейная зависимость между входной и выходной величинами (рис. А). Коэффициент пропорциональности между ними называется коэффициентом передачи звена. Этот коэффициент безразмерен, если размерности входной и выходной величин одинаковы.

Интегрирующими называются звенья, в которых в установившемся режиме линейная зависимость связывает входную величину и производную выходной величины (рис. Б). В этом случае выходная величина пропорциональна интегралу по времени от входной величины, чем и обусловлено название звена. Коэффициент передачи звена имеет в этом случае размерность с^-1, если размерности входной и выходной величин одинаковы.

К дифференцирующим относятся звенья, в которых в установившемся режиме выходная величина пропорциональна производной по времени от входной величины.(рис. В). Коэффициент передачи звена имеет размерность секунды, если размерности входной и выходной величин одинаковы.

 

 

 

Приведённые на рис. зависимости относятся к установившимся режимам работы звеньев т.е. являются статическими характеристиками этих звеньев.